선택정렬(Selection sort), 삽입정렬(Insertion sort), 거품정렬(Bubble sort)는 평균 시간 복잡도가 O(N^2) 이고 빠른정렬(Qick sort), 합병정렬(Merge osrt), 힙정렬(Heap sort) 은 O( n log n )이였다.
반면 계수정렬(Counting Sort)는 다른 정렬 알고리즘보다 좀 더 빠른 O(n)의 성능을 보여준다.
그럼 다른 정렬알고리즘 보다 빠르다고하니 계수정렬만 사용하면 되는거 아닌가 ? 라고 생각할 수 있는데 계수정렬은 특정 상황에서만 사용해야하는 제약이 따른다.
계수정렬 알고리즘을 살펴보자. 계수정렬은 기본적으로 원소들의 빈도를 카운트하여 정렬하는 방법이다.
빈도를 카운트하여 정렬한다는게 이해하기 어려울수 있으니 그림을 보면서 이해하자.
그림1 과 같이 N = 8개인 배열 A = { 5, 3, 0, 2, 4, 1, 0, 5, 2, 3, 1 } 가 있다고 하자.
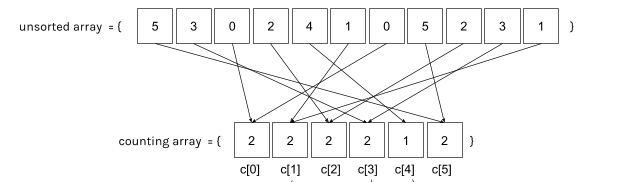
계수정렬은 젤 먼저 정렬되지 않은 배열의 인덱스를 0부터 N-1 까지 하나하나 지나가면서 각 원소의 값이 몇 번 나왔는지 카운트하여 별도의 카운팅 배열(counting array)에 저장한다.
예를들어 그림1의 정렬되지 않은 배열의 값은 카운팅배열의 인덱스(index)가 되고 그 인덱스의 값을 +1 (카운팅) 해주면 각 숫자의 빈도가 몇개인지 알 수 있을 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public class HelloWorld {
public static void main(String[] args) {
int []unsortedArray = { 5, 3, 0, 2, 4, 1, 0, 5, 2, 3, 1 };
int []countingArray = new int[6];
for(int i = 0 ; i < unsortedArray.length ; i++) {
countingArray[unsortedArray[i]]++;
}
for(int j = 0 ; j < countingArray.length ; j++) {
System.out.println(String.format("number = %d, count = %d", j, countingArray[j]));
}
}
}
// output
number = 0, count = 2
number = 1, count = 2 number = 2, count = 2 number = 3, count = 2 number = 4, count = 1 number = 5, count = 2 Colored by Color Scripter
|
이제 카운팅 소트로 정렬을 할 텐데 어떻게 해야 할까 ?
조금만 생각해 보면 카운팅된 배열 인덱스번호가 원래 정렬되지 않은 배열 원소의 숫자이고 그 값이 숫자의 총 개수다.
즉, countingArray[0] = 2 라면 number = 0 이 2개 있다는 뜻이다.
따라서 countingArray[0] 부터 countingArray[countingArray.length-1] 까지 인덱스(number)별 숫자 개수를 출력하면 정렬이 된다.

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public class HelloWorld {
public static void main(String[] args) {
int []unsortedArray = { 5, 3, 0, 2, 4, 1, 0, 5, 2, 3, 1 };
int []countingArray = new int[6];
// 숫자의 빈도를 카운팅하여 카운팅배열에 저장한다.
for(int i = 0 ; i < unsortedArray.length ; i++) {
countingArray[unsortedArray[i]]++;
}
// 카운팅배열의 index 는 정렬되지 않은 배열의 숫자(number)이고 값은 숫자의 총 개수이니
// 개수만큼 index 를 출력하면 정렬된 값이 출력된다.
for(int c = 0 ; c < countingArray.length ; c++) {
if(countingArray[c] > 0) {
for(int k = 0 ; k < countingArray[c] ; k++) {
System.out.print(c + " ");
}
}
}
}
}
Colored by Color Scripter
|
어라 카운팅 정렬 너무 간단한데라고 생각할 수 있으나 아직 끝난 건 아니다.
사실 배열의 원소가 특정 범위의 숫자(number)나 문자(character)로만 되어 있다면 여기까지만 해도 카운팅 정렬을 이용해서 선형시간내에 정렬이 가능하다. 하지만 몇가지 의심을 해야 한다.
Q. 빈도를 저장할 배열의 크기를 얼마나 잡아야 하는가 ?
배열원소가 출현하는 빈도를 카운팅해서 카운트배열에 저장해야 하기 때문에 계수정렬은 빈도를 저장하기위한 메모리가 추가로 필요로한다. 메모리는 적게 사용되도록 해야 하는데
k 값이 정해져있다면.. 또는 range 가 정해져 있다면 .. 아니면 max 값 을 구해야함. max 값 구할때 min 값도 구하면 좋겠다.배열원소가 출현하는 빈도를 카운팅해서 배열에 저장해야 하기 때문에 계수정렬은 빈도를 저장하기 위한 메모리가 추가로 필요하다.
메모리는 적게 사용할수록 좋은데 만약 입력되는 비정렬 배열 원소들이 숫자 0-9로만 되어 있거나 문자 a-z 로만 되어 있다면 숫자 10, 알파벳 26개를 카운팅할 수 있는 메모리만 필요로하니 상관없으나 만약 입력의 자료가 매우 크고(N개) 어떤 숫자들이 들어 올지 모른다면 어쩔수 없이 최대값(max) 이나 최소값(min) 을 찾고 max-min+1 만큼만 메모리를 할당해야 할 것이다.
문제는 2가지가 있는데 max, min 을 찾기위한 추가적인 연산이 필요하게 되고, 입력된 배열의 숫자가 A = { 1, 3000002, 3000000 } 처럼 A배열의 개수는 3개 지만 min - max의 차이는 커지기 때문에 위 방식처럼 min-max+1만큼 메모리를 할당하면 개수는 3개인 반면 메모리는 쓸데 없이 많이 차지하게 되는 꼴이 발생하게된다.
따라서 카운트정렬은 N개의 정수를 정렬하는데 단 모든 정수는 0 - k사이의 정수이고 위 예제처럼 그 범위가 너무 크지 않은 곳에 적용하는것이 좋다. 즉 정렬할 원소값의 range가 작고 한정적인곳에 좋은 성능을 보일수 있다는 것이다
Q. 만약 정렬하려는게 숫자가 아니고 객체라면 ?
아래와 같은 학생들의 알고리즘 과목 시험점수 데이터가 있고 시험점수 순으로 정렬한다고 하자
시험점수가 동일한 값이 있을때 입력에 먼저 나오는 값이 출력에서도 먼저 나오도록(stable sort)하도록 해야 한다면 위 방식으로 했을 때 stable sort 를 보장하기 힘들다.
| name | score |
| Jack | 90 |
| Harry | 90 |
| Jacob | 80 |
| Charlie | 80 |
| George | 90 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
public class HelloWorld {
public static class AlgScore {
public String name;
public int score;
public AlgScore(String name, int score) {
this.name = name;
this.score = score ;
}
}
public static void main(String[] args) {
AlgScore []unsortedArray = {
new AlgScore("Jake", 90),
new AlgScore("Harry", 80),
new AlgScore("Jacob", 80),
new AlgScore("Charlie", 90),
};
int []countingArray = new int[101]; // 0점부터 100점
// 점수 빈도를 카운팅하여 카운팅배열에 저장한다.
for(int i = 0 ; i < unsortedArray.length ; i++) {
countingArray[unsortedArray[i].score]++;
}
// 카운팅배열의 index 는 정렬되지 않은 배열의 숫자(number)이고 값은 숫자의 총 개수이니
// 개수만큼 index 를 출력하면 정렬된 값이 출력된다.
AlgScore sortedArray[] = new AlgScore[unsortedArray.length];
for(int c = 0 ; c < countingArray.length ; c++) {
if(countingArray[c] > 0) {
for(int k = 0 ; k < countingArray[c] ; k++) {
// 점수가 동일하면 누구의 점수인지 어떻게 알아야 하는가 ?
// 입력된 순서대로 나오게 하려면 방법은 있지만 좀 비효율적이다.
... ?
}
}
}
}
}
Colored by Color Scripter
|
대부분의 경우 정렬할 키값 들은 클래스 변수중 일 부분(여기서는 시험점수)이기 때문에 해당 키값이 어느 객체를 지정하여 정렬해야 할 다른 방법이 필요하다.
계수정렬에서는 일단 이 것을 해결하기 위해 그림3 과 같이 카운팅 배열 빈도수의 누적합을 구한다.
즉, 카운팅 배열을 수정하여 각 인덱스에 빈도수와 이전 빈도수으 누적 합계를 저장한다.
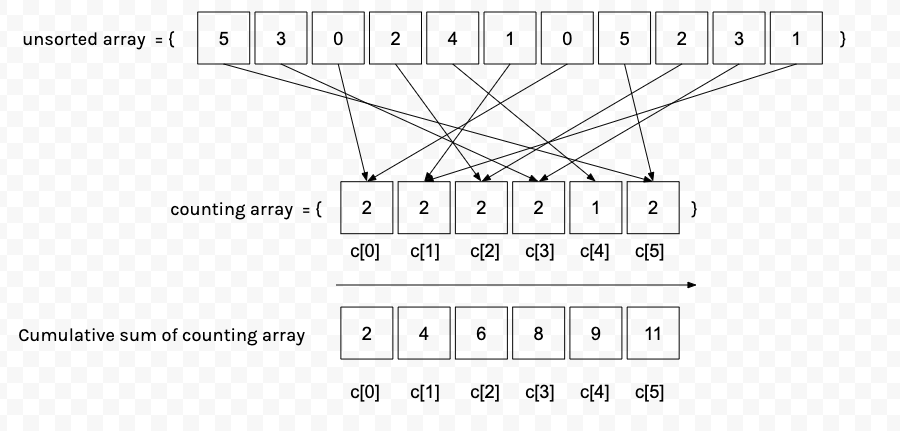
수정된 누적된 배열의 index는 우리가 비교하려던 키값이고 누적값은 입력된 데이터 원소가 정렬시 배치되어야할 index 값이다.
말이 좀 어려운데 그림3에서 unsorted array[0] = 5 는 누적된 배열 인덱스의 키값이다.
즉, unsorted array[0] = 5 -> 5를 누적된배열 인덱스의 키값으로 한다. Cumulative sum of counting array[5] = 11 을 얻는데 11은 11번째 위치되어야 한다는 것이다.
그리고 동일한 값이 나온경우 이미 차있는 11번재 배치할수 없으니 11 번째 이전에 배치되도록 -1을 감소시켜준다.
그림4 과정을 설명하면 정렬되지않은 배열(unsorted array)를 A라고하고 카운팅배열에서 빈도수 누적합을 구한 Cumulative sum of counting array를 B라하고, 최종적으로 정렬된 데이터가 배치될 배열(sorted arrya)을 C라고 할때
stable sort를 위해 A배열을 뒤부터 수행한다.
-> A[A.lenght-1] = 1 -> B[1] = 4 -> C의 4번째에 배치되어야 한다는것을 알고있음. 배열은 zeoro-base 이니 B[4 - 1(zero-base)] = A[A.lenght-1] 를 넣어준다.
그리고 B[1] = 4 는 number=1을 가진 원소는 4번째 위치해야한다는 뜻인데 이미 배치를 했으니 다음에 number=1이 나오면 중복되니 B[1] = B[1] -1 을 해주어야 한다.

최종 구현 코드는 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public class HelloWorld {
public static class AlgScore {
public String name;
public int score;
public AlgScore(String name, int score) {
this.name = name;
this.score = score ;
}
}
public static void main(String[] args) {
AlgScore []unsortedArray = {
new AlgScore("Jake", 90),
new AlgScore("Harry", 80),
new AlgScore("Jacob", 80),
new AlgScore("Charlie", 90),
};
int []countingArray = new int[101]; // 0점부터 100점
// 점수 빈도를 카운팅하여 카운팅배열에 저장한다.
for(int i = 0 ; i < unsortedArray.length ; i++) {
countingArray[unsortedArray[i].score]++;
}
// 누적합을 구한다.
for(int i = 1 ; i < countingArray.length ; i++) {
countingArray[i] += countingArray[i-1];
}
AlgScore sortedArray[] = new AlgScore[unsortedArray.length];
// 입력된 순서대로 출력하기위해서(stable sort) 뒤부터 (reverse) 정렬해준다.
for(int i = unsortedArray.length - 1 ; i >= 0 ; i--) {
// 수정된 누적된 배열의 index는 우리가 비교하려던 키값이고 누적값은 입력된 데이터 원소가 정렬시 배치되어야할 index 값이다.
// 동일한 값이 나온경우 이미 차있는 위치에 배치할수 없으니 이전에 배치되도록 -1을 감소시켜준다.
sortedArray[countingArray[unsortedArray[i].score] -1] = unsortedArray[i];
--countingArray[unsortedArray[i].score];
}
for(int i = 0 ; i < sortedArray.length ; i++) {
System.out.println(String.format("name=%s, score=%d", sortedArray[i].name, sortedArray[i].score));
}
}
}
Colored by Color Scripter
|
카운팅정렬은 선형시간내 정렬을 할 수 있지만 추가적인 메모리(숫자 개수를 저장할 공간, 결과를 저장할 공간)가 필요하기 때문에 입력 원소의 범위(rage)를 모르거나 값의 차이가 크면 효율성이 떨어진다는 단점이 있다.
레퍼런스
'알고리즘(Algorithm) > 정렬(Sorting)' 카테고리의 다른 글
| 정렬(Sorting)이란? (0) | 2019.07.08 |
|---|---|
| 퀵정렬(Quick Sort) (0) | 2019.07.04 |
| 버킷정렬(Bucket Sort) (0) | 2019.07.01 |
| 기수정렬((Radix Sort) (0) | 2019.06.19 |
| 힙정렬(Heap Sort) (1) | 2019.06.19 |



