퀵정렬은 매우 효율적인 정렬 알고리즘이며 데이터 배열을 특정 규칙에 의해 분할 하면서 정렬을 하는 분할정복(Divide & Conquer) 에 기반한다.
분할단계에서는 배열은 다음과 같은 조건이 만족되도록 2개의 부분으로 나누는데 그 중 하나는 지정된 값보다 작은 값들로 다른 하나는 지정된 값보다 큰 값들로 이루어지도록 분할한다.
여기서 지정된 값을 보통 피벗(pivot)이라고 불린다.
즉, 분할되기전 배열에서 임의의 기준값이 될 피벗을 하나 선택한다. 피벗을 배열중에 어떤 놈을 선택할지는 나중에 설명하겠다. 지금은 그냥 배열에 아무값이나 선택한다고 생각하면 된다. 지금은 일단 배열의 맨 끝에 있는 놈을 피벗으로 선택한다.
다음 그림에서 ①번은 아직 정렬되지 않은 배열데이터를 나타내고 ②번은 맨 끝에 있는 놈을 피벗으로 선택한 것이다.
피벗을 선택하였으면 분할을 해야하는데 ③번 처럼 피벗보다 작은 값은 왼쪽으로 이동하고 큰 값은 오른쪽으로 이동하도록 하면된다.

▲ [출처] https://medium.com/basecs/pivoting-to-understand-quicksort-part-1-75178dfb9313
여기까지 qicksort 알고리즘으로 보면 의사코드는 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public static qicksort(A[], left, right) {
if( left < right) then {
q = partition(A, left, right); ▷ 분할
qicksort(A, p, q-1); ▷ 왼쪽 부분배열 정렬
qicksort(A, q+1, r); ▷ 오른쪽 부분배열 정렬
}
}
public static partition(A[], l, r) {
배열 A[l ... r]의 원소들을 A[r] = 피봇 기준으로 양쪽으로 재배치하고
A[r]이 자리한 위치를 리턴한다. }
Colored by Color Scripter
|
그럼 분할을 어떤 방식으로 해야하는지 알고리즘을 자세히 살펴보자.

피봇을 A의 마지막값으로 설정하고 (여기서는 5가 된다.) 배열의 젤 앞을 low 로 그리고 피봇을 뺀 마지막 인덱스를 high로 하고
i 를 low - 1 로 하는데 여기서 i 가 하는 역할은 파티션하면서 좌측에는 피봇보다 작은값들이 우측에는 피봇보다 큰 값들로 나뉘어 질텐데 작은값들이 있는 맨 마지막 인덱스를 가리킬것이다.(즉 피봇보다 처음으로 큰값이 나타나는 index - 1 의 위치이다.)
처음에는 작은값이 아무것도 없으므로 일단 low 보다 -1 을 해주면 된다.
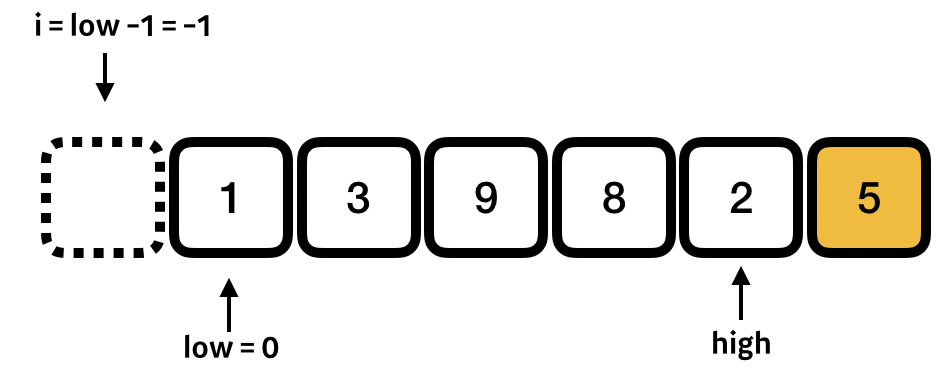
이제 low 부터 ~ high 까지 for 루프를 돌면서 피봇값과 하나씩 비교해본다.
젤 처음 1은 피봇 5보다 작으므로 작은 값이 있는 위치 i 를 하나 증가시켜준다.

두번째 3도 피봇 5보다 작으므로 위치 i 를 하나 증가시켜준다.
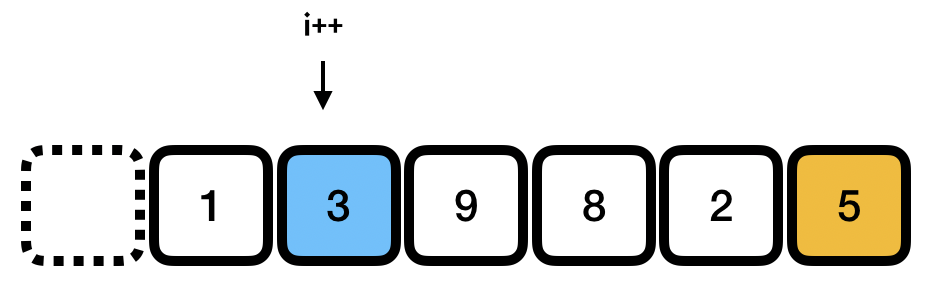
이제 9랑 8을 차례차례 비교해보면 피봇보다 크므로 i는 증가시키지 않고 그냥 그대로 있는다
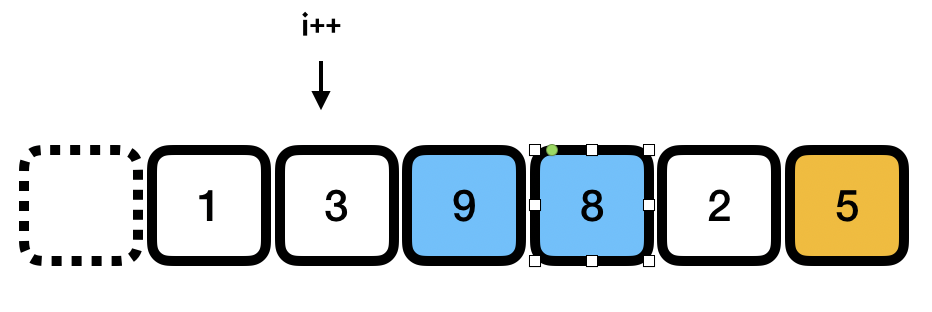
2차례인데 2는 피봇 5보다 작으므로 i를 하나 증가시켜주고 i에 있는 9와 2를 서로 swap 해준다.
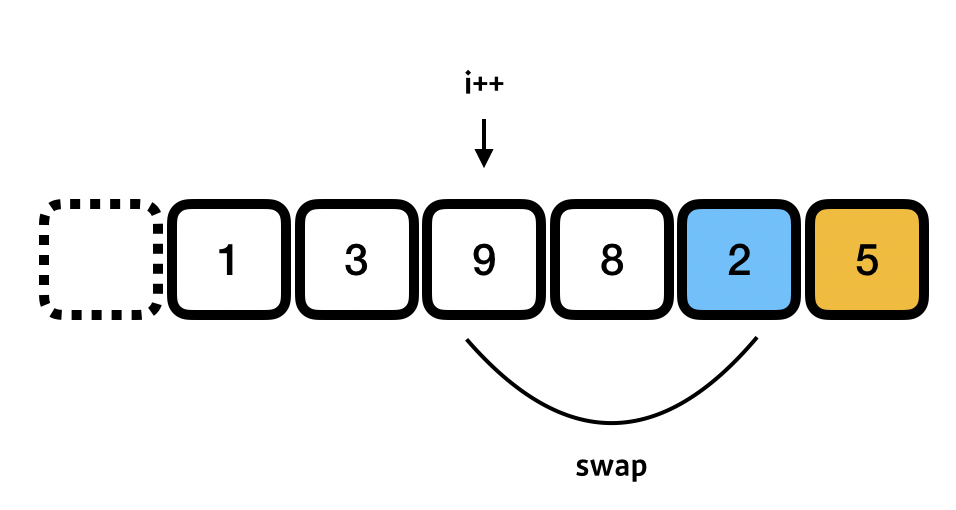
여기까지 왔으면 피봇을 제외하고 i 보다 같거나 작은 index 들에는 피봇보다 작은 값들이 그리고 큰 index 에는 큰 값들로 분리되어 있을 것이다. 마지막으로 피봇을 이동시켜야 하는데 피봇보다 큰 값들이 젤 처음 나타나는 위치와 서로 스왑하면 된다.
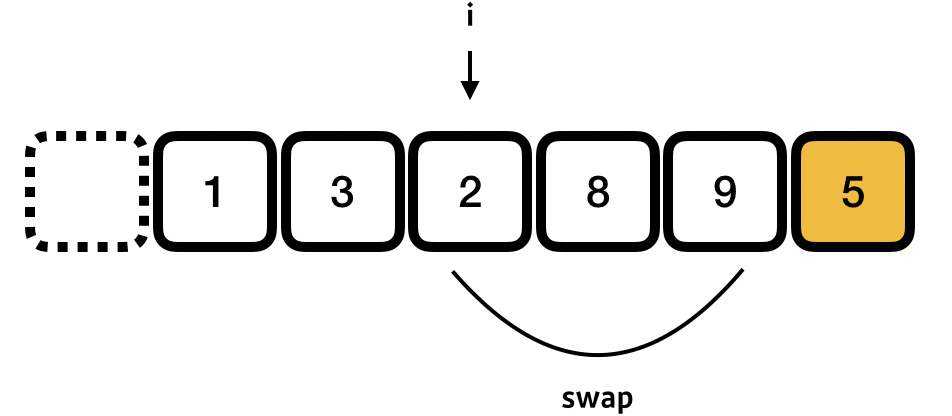
피봇보다 큰값이 젤 먼저 나오틑 위치는 현재 i+1 = 8 이며 이 위치와 피봇의 위치를 서로 swap 해준다.

최종적으로 좌측은 pivot 보다 작은 배열들로, 우측은 큰 배열로 분할 된 것을 보여준다.

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
public class QuickSort {
private QuickSort() { }
public static void sort(Comparable[] a) {
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
private static int partition(Comparable[] a, int lo, int hi) {
// pivot 보다 작은 값들로 채워진(왼쪽배열) 맨 마지막 index
int i = lo - 1;
// 피봇은 맨 끝 값으로 선택.
Comparable pivot = a[hi];
for(int j = lo ; j < hi ; j++ ) {
// a[j]가 pitvot 보다 작다면 a[i] 와 a[j]를 swap 한다.
if(less(a[j], pivot)) {
// pitvot 보다 작은 값으니 개수를 +1 해주고 작은값을 현재 왼쪽배열의 마지막으로 swap
i++;
swap(a, i, j);
}
}
// 피봇보다 큰 값이 젤 처음 나타나는 위치 i+1 과 서로 swap 한다.
swap(a, i+1, hi);
return i+1;
}
// v 가 보다 작으면 tue, 그렇치 않으면 false
private static boolean less(Comparable v, Comparable w) {
if (v == w) return false; // optimization when reference equals
return v.compareTo(w) < 0;
}
// 두개의 값을 swap 한다.
private static void swap(Object[] a, int i, int j) {
if( i == j)
return;
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
Integer array[] = { 31, 8, 48, 73, 11 , 3, 20, 29, 65, 15} ;
// 3 8 11 15 20 29 31 48 65 73
.map(i -> String.valueOf(i))
.collect(Collectors.joining(" ")));
}
Colored by Color Scripter
|
'알고리즘(Algorithm) > 정렬(Sorting)' 카테고리의 다른 글
| 정렬(Sorting)이란? (0) | 2019.07.08 |
|---|---|
| 계수정렬(Counting Sort) (0) | 2019.07.08 |
| 버킷정렬(Bucket Sort) (0) | 2019.07.01 |
| 기수정렬((Radix Sort) (0) | 2019.06.19 |
| 힙정렬(Heap Sort) (1) | 2019.06.19 |



