지난 강좌에서는 버블정렬(Bubble Sort), 선택정렬(Selection Sort), 삽입정렬(Insertion Sort)와 같이 비교적 간단하고 이해하기 쉬우나 큰 데이터 셋에는 효율적이라고 할 수 없는 기본적인 정렬 알고리즘에 대해서 알아 봤었다.
이번 시간에는 분할정복 알고리즘을 통해 정렬이 이루어지는 합병정렬(Merge Sort)에 대해서 설명하겠다.
분할정복 알고리즘 개념이 필요하니 분할정복(Divide & Conquer) 알고리즘 을 반드시 읽어 봐야 한다.
합병정렬을 하기위해 예를들어 아래와 같은 데이터가 있다고 하자.

합병정렬은 먼저 데이터 크기가 1개가 될때 까지 반복하여 같은 반으로 나누는 분할 단계를 거친다.
여기서는 8 개 항목의 배열을 크기가 4인 배열로 분할한다.

크기가 4개인 배열 2개는 원래 배열의 순서와 크게 다르지 않고 배열이 2개로 쪼개진것 뿐이다.
아직 크기가 1개가 아니므로 다시 반으로 분할한다.

더 이상 쪼개질 수 없을 때까지 계속 나누면 결국엔 1개의 원소를 가진 배열 8개짜리로 분할 된다.

이제 분해 된 것과 똑같은 방식으로 문제를 해결하면서 병합하기 위해서 먼저 각 목록의 요소를 비교 한 다음 이를 정렬 된 방식으로 다른 목록에 결합하면 돤다.
14와 33을 병합한 결과는 이미 정렬 상태라 다음 27과 10을 비교해 본다.
2개의 값의 대상 목록에서 먼저 10을 넣고 27을 따르도록 병합한다.
그 다음 19와 35의 순서를 바꾸는 반면 42와 44는 순차적으로 나열하여 병합하면 첫 번째 병합을 위한 단계가 끝난다.

병합 단계의 다음 반복에서는 두 개의 데이터 값 목록을 비교하여 이를 모두 정렬 된 순서로 배치 된 목록으로 병합한다.

최종적인 병합 모습은 아래와 같게 된다.

위의 설명을 좀더 이해하기 쉽도록 종합적인 알고리즘을 아래 그림을 토대로 구현을 할 것이다.

▲[출처] https://www.java67.com/2018/03/mergesort-in-java-algorithm-example-and.html
알고리즘을 구현하기 위해 원래 정렬되지 않은 배열(unsorted array)를 크기가 1이 되도록 분할(divide)하는 것은 배열을 반씩 쪼개면서 재귀적으로 호출(1 부터 3단계) 하면 되는데
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public static void mergeSort(int []list, int p, int r) {
// 배열의 크기가 1이 될 때 까지 재귀적으로 호출하여 분할한다.
if( p < r) {
int q = (p + r)/2;
// 분할된 좌측은 mergeSort 를 재귀적으로 호출하여 배열의 크기가 1이 될 때 까지 계속 호출한다.
mergeSort(list, p, q);
// 분할된 우측도 mergeSort 를 재귀적으로 호출하여 배열의 크기가 1이 될 때 까지 계속 호출한다.
mergeSort(list, q+1 , r);
merge(list, p, q, r);
}
}
// 분할된 것을 정렬하면서 합병하는 함수이다.
private static void merge(int []list, int p, int q, int r) {
}
Colored by Color Scripter
|
문제는 분할 한 것을 정렬(sort) 하고 어떻게 병합(merge) 하느냐 (4-6단계) 이다.
생각해보면 분할된 배열들은 이미 정렬된 상태일 것이기 때문에 정렬된 2개의 배열을 하나로 합치기 위해서는 정렬된 2개의 배열을 처음부터 하나씩 비교해 가면서 작은값 또는 큰 값순서대로 하나씩 빼서 임시배열에 배치하고 원래 정렬되지 않은 배열에 merge 된 임시배열값을 복사해주면 된다.
예를들어 분할된 X 와 Y의 2개 배열이 있고 X, Y는 1개의 원소를 가진 배열이 -> 2 -> 4개 크기로 merge 되면서 이미 정렬된 상태로 되어 있다고 가정하자.
이제 4개의 크기를 가진 X, Y 배열을 8개로 합병하기위해 8개 크기(int a[8] ) 를 가진 임시배열 Result 를 생성한다.
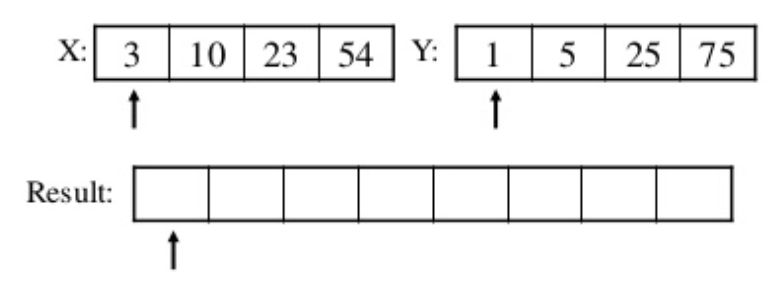
X배열의 첫번째 값 3과 Y배열의 첫번째 값 1을 서로 비교하여 둘중에 작은 것을 Result 의 첫번째에 넣어준다.
둘중에 1이 더 작기 때문에 Result 첫번째에 1이 들어갔고 이제 다음 비교를 위해 Y배열의 비교 위치를 한칸 뒤로 이동한다.

X[0] = 3과 Y[1] = 5를 비교하면 X[0] < Y[1] 이기 때문에 X[0] 의 값을 Result[1] = X[0] 으로 넣어준다.

이번에는 X[0] 이 Result[1]로 들어갔기 때문에 다음값을 비교하기위해 X 배열의 비교 위치를 한칸 뒤로 이동한다.
X[1] = 10 > Y[1] = 5 이기 때문에 Result[2] = Y[1] 이 된다.
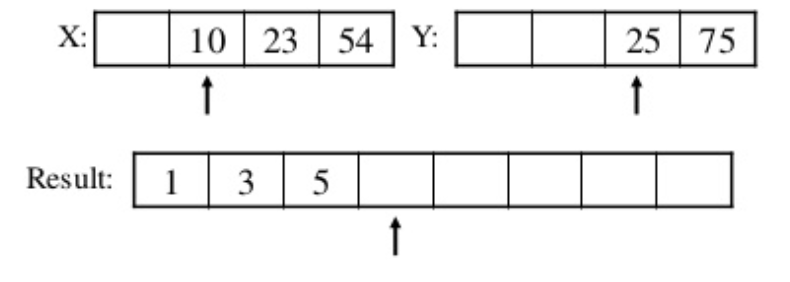
이렇게 계속 비교해가면서 X, Y 의 비교 위치를 이동하고 Result 값을 채워 나가면 결국엔 Result 의 모든 원소는 정렬된 상태로 되고 2개의 배열의 병합(merge)이 끝나게 된다.

이제 merge 함수를 구현해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
public class Main {
public static void main(String[] args) {
int array[] = {14, 33, 27, 10, 35, 19, 42, 44};
mergeSort(array, 0, array.length-1);
for (int i = 0 ;i < array.length ; i++){
System.out.print(array[i] + " ");
}
}
public static void mergeSort(int []list, int start, int end) {
// 배열의 크기가 1이 될 때 까지 재귀적으로 호출하여 분할한다.
if( start < end) {
int mid = (start + end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1 , end);
merge(list, start, mid, end);
}
}
private static void merge(int []list, int start, int mid, int end) {
// 병합할 것은 2개의 배열이다.
// 1. start ~ mid 까지 X 배열
// 2. mid+1 ~ end 까지 Y 배열
// 병합한 후 정렬된 값을 임시로 저장할 배열을 선언한다.
int result[] = new int[list.length] ;
// X와 Y배열의 맨 처음 index 부터 서로 값을 비교할 위치 변수
int xs = start, ys = mid+1;
int k = start;
while(xs <= mid && ys <= end) {
// 배열 2개의 값을 처음부터 비교하여 작은 값을 result 에 넣는다.
if(list[xs] <= list[ys]) {
// X 배열이 작기 때문에 다음에 비교할 값의 index를 한칸 뒤로 이동한다.
result[k++] = list[xs++];
}
else {
result[k++] = list[ys++];
}
}
/*
X, Y 값을 비교하다보면 X나 Y의 비교 index 가 끝까지 이동 못하는 경우가 있다.
예를들어
X = { 1, 3, 5, 6} 이고 Y = { 4 , 7, 10, 12} 라고 한다면
while 이 끝나고 각 배열은 아래처럼 되어 있다.
X = {}, Y = { 7, 10, 12} result = { 1, 3, 4, 5, 6 }
어느쪽이던 남아 있는것을 result 뒤에 모두 이동시키면 병합이 되기 때문에
X 에 남아 있다면 X에 남아 있는 모든 원소를 result 에 넣어주고
Y 에 남아 있다면 Y에 남이 있는 모든 원소를 result 에 넣어주면 된다.
*/
while( xs <= mid) {
result[k++] = list[xs++];
}
while( ys <= end) {
result[k++] = list[ys++];
}
// 임시로 생성한 result 를 원래 배열 list 에 assign 해준다.
for( int i = start ; i <= end ; i++) {
list[i] = result[i];
}
}
}
Colored by Color Scripter
|
코드중에서 정렬되지 않은 워래 list 배열에 정렬된 것을 넣어버리면 나머지 분할, 병합시 원소가 잘못 들어가지 않을까? 궁금해 할수 있는데
다음 그림처럼 재귀 순서를 보면 항상 좌측부터 우측으로 분할되고 합병되기 때문에 문제가 없다.

▲ [출처] : https://www.geeksforgeeks.org/merge-sort/
레퍼런스
'알고리즘(Algorithm) > 정렬(Sorting)' 카테고리의 다른 글
| 기수정렬((Radix Sort) (0) | 2019.06.19 |
|---|---|
| 힙정렬(Heap Sort) (1) | 2019.06.19 |
| 삽입정렬(Insertion Sort) (0) | 2019.06.19 |
| 버블(거품)정렬(Bubble Sort) (0) | 2019.06.19 |
| 선택정렬(Selection Sort) (0) | 2019.06.18 |



