서로소집합에 대한 개념은 위키백과에 너무 잘 설명되어 있어 위키백과를 기준으로 개념을 알아보자.
Q. 서로소집합(Disjoint Set : 디스조인트 셋) 은 무엇인가 ?
서로소 집합이란 우선 집합이란 단어가 들어 갔으니 수학적으로 집합 개념일 것이다.
수학적으로 집합의 개념을 컴퓨터에서는 자료구조 셋(Set)으로 표현할 수 있다.
나중에 설명하겠지만 서로소집합의 자료구조는 원래 집합 자료구조인 셋(Set)과는 다르게 트리로 구성된다.
오키 그러니 집합이라 했으니 그림1 처럼 생겼겠구나 생각하면 된다.
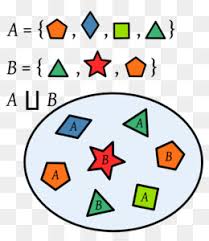
그럼 집합은 집합인데 서로소(disjoint)는 또 무엇일까? 디스조인트란 말은 서로 공통적인 원소가 없다는 것이다. 서로서로 각자 다르다.
예를들어 그림2. 집합개념에서 좌-상단이 Disjoin sets 을 나타내는것인 집합 A 와 집합 B의 교집합, 즉, 공통적인 원소가 전혀 없는 것이다.
위 그림1. 집합에서도 자세히 보면 아기자기한 도형들을 포함한 집합 A, B는 교집합 원소가 1개도 없다. 즉 그림1 도 서로소집합이다.

즉, 서로소집합은 한개의 집합으로는 성립되지 않고 집합이 여러개있을때 서로서로 공통적인 원소가 없어 모든 집합의 교집합은 공집합( Φ )이 된다는 말이다.
Q. 서로소집합을 표현하기위해 트리를 사용한다고 하였는데 ? 트리로 ?
뭐 대단한 개념은 아니고 그냥 집합의 원소들이 서로 연결된 트리(이진트리던 BST던 일반트리던 상관없다) 로 되어 있다는 말이다.
트리로 연결된 모든 노드(원소)들은 같은 집합에 속해 있다고 보면된다,
예를들어 S1 ∈ { 1 }, S2 ∈ { 2 }, S3 ∈ { 3 } , S4 ∈ {4 }, S5 ∈ {5 } 이렇게 S1 ~ S5 집합이 5개 있다면 노느 하나짜리 트리가 된다.

[출처] : https://www.techiedelight.com/disjoint-set-data-structure-union-find-algorithm/
그림3 을 보면 각 집합이 가지고 있는 원소는 모두 다르다(서로소 = Disjoint)하다.
사실 그림3은 트리처럼 보이지 않으니 그림4로 봐야 좀더 이해가 쉽겠다.
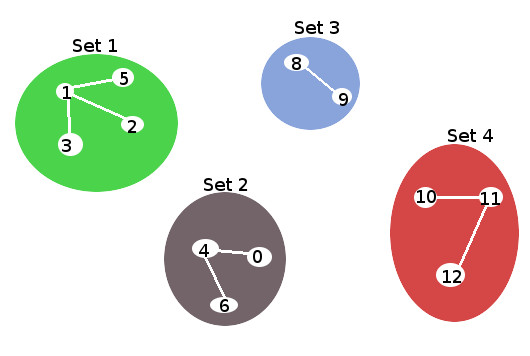
그림4도 각 집합들을 자세히 보면 공통인 원소가 없으니 서로소집합이 된다.
Q. POST 타이틀은 서로소집합(Disjoint Set) - 합집합-찾기(union–find) 인데 합집합-찾기는 도대체 무엇인가?
서로소 집합도 집합이니 집합 연산이 필요한데 서로수집합은 서로 공통원소가 없으니 차집합, 교집합은 의미가 없다.
차집합 교집합을 해봤자 다 공집합이기 때문이다.
따라서 합집합만 있으면 될것 같은데 서로소집합에서 합집합을 찾는 것을 disjoint set - 유니온(Union) 이라 하고
각 원소에가 트리의 어떤 루트노드에 연결되어 있는지 그 루트를 찾는 연산을 disjoint set - 파인드(Find) 라 부른다.
뭐 알고리즘명이 명확해서 이해는 잘 간다.
그럼 union 은 어찌 하면될까 ? 그림3 에서 S3 ∈ { 3 } ∪ S4 ∈ {4 } = { 3, 4 } 인데 그냥 합집합하려는 집합 S4의 루트노드를 S3 트리노
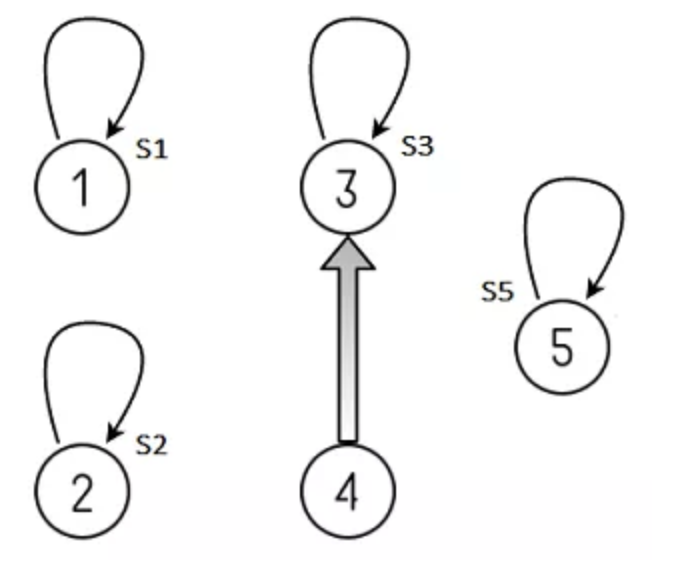
드중 아무곳이나 자식노드로 추가하면된다. 그림5는 S3 트리노드에 S4의 루트노드를 자식으로 추가한것이다.
합집합을 한 후에도 모든 집합은 disjoint 상태임이 확인된다.

그림 6은 S1 ∈ { 1 } ∪ S2 ∈ { 2 } = { 1, 2 } 가된 후 다시 S3 와 합집합을 수행한 후 이다.
파인드(find)는 해당 원소가 포함된 집합의 루트 노드를 반환하면된다.
트리로 되어 있으니 루트노드를 찾는건 부모가 없을때까지 재귀적으로 찾으면 될 것이다.
|
1
2
3
4
|
function find(x)
if x.parent != x
x.parent := find(x.parent)
return x.parent
|
Q. 도대체 어디에 사용되는 자료구조인 & 알고리즘인가 ?
위키에 응용부분을 보면 서로소 집합 자료구조는 집합의 분할을 모델링한다. 예를 들어 이 자료구조를 활용하여 무향 그래프(undirected graph)의 연결된 요소들을 추적 할 수 있다. 그리고 이 모델은 두 개의 꼭짓점(vertex)들이 같은 요소에 속하는지 또는 그 꼭짓점들을 엣지(edge)로 연결 할 때 싸이클(cycle)이 발생하는지 등을 결정 할 수 있다고 나와있다.
따라서 최소신장트리(Minimum Spanning Tree)를 생성하기 위한 크러스컬(Kruskal) 알고리즘 에서 서로수집합(Disjoint Set)의 합집합-찾기(union-find) 자료구조 & 알고리즘이 사용되는데 왜냐면 최소신장트리(MST)는 모든 정점이 연결되어(connected)있어야 하고 연결된 정점간 사이클이 존재하면 안되는데 각 정점을 연결할때 사이클이 있는지 없는지 체크할때 사용된다.
Q. 트리로 disjoint sets 자료구조를 표현한다 하였는데 구체적으로 ?
이진트리도 노드 or 배열로 표현가능한것처럼 서로수집합 구현은 트리로 구성되서 뭔가 트리자료구조 처럼 노드가 연결된 것처럼 구현할 수 도있 지만 UNION-FIND만 있으면되기 때문에 배열로도 표현가능하다.
그림7의 (a)는 S1 ∈ { 1 }, S2 ∈ { 2 }, S3 ∈ { 3 } , S4 ∈ {4 }, S5 ∈ {5 } ..... S10 ∈ { 10 } 인 서로수 집합을 배열로 표현한건데
배열의 인덱스는 NIUMBER는 (여기서는 제로베이스가 아니라고 가정) 루트노드의 번호가 되고 각 배열의 값은 차일드 노드값들이 된다.
하지만 처음 각 집합은 하나의 원소들만 가지고 있고 자기자신이 원소이면서 루트로드이기 때문에 배열 U[1] .. U[10]까찌 self 넘버가 들어가있다.
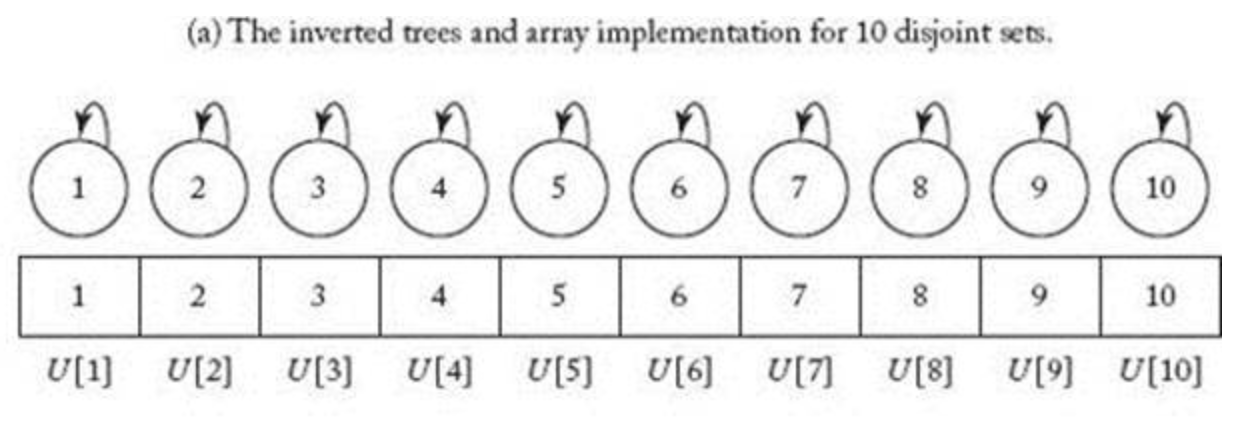
그림8은 S4 ∪ S10 = { 4, 10 } 이 되었고 S10이 가지고 있던 루트노드는 S4의 누르토드 자식으로 추가되었다
그럼 10원소의 부모노드가 10이였던 것이 4로 바뀌었으므로 U[10] = 4로 업데이트 된 것이다.
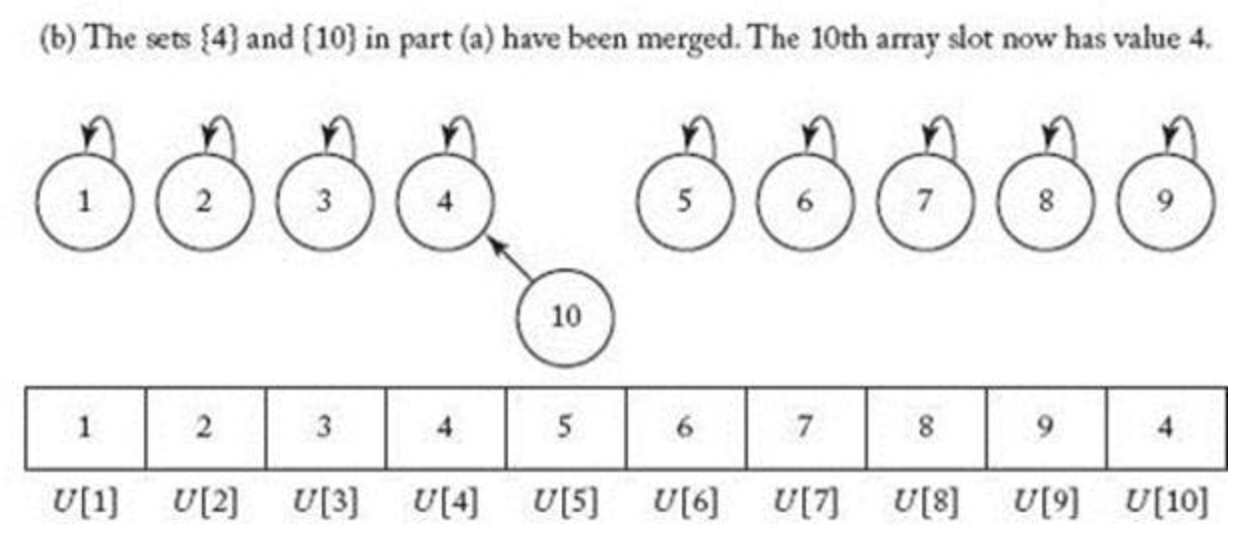
즉 각 배열의 값에는 내가 어떤 노드의 자식으로 되어 있는지를 나타내면 된다.
좀더 복잡한(?) 예를 들어보면 그림 9와 같다.
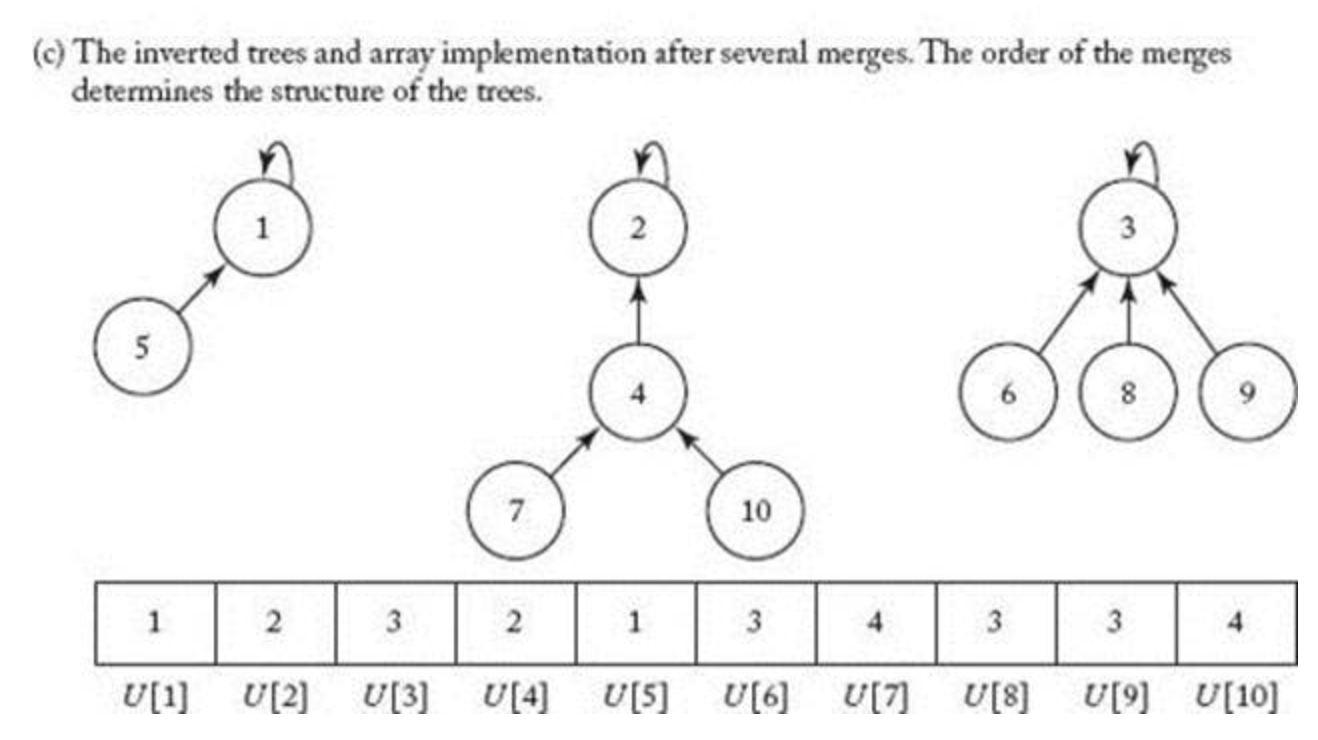
[출처] https://apprize.info/science/algorithms/15.html
S1 의 자식노드 5는 부모노드가 1이기 때문에 U[5] = 1로 되어있고
S2 의 자식노드중 7은 부모 노드가 4이기 때문에 U[7]은 4로 되어 있다.
이렇게 되어 있으면 7이 어느 집합의 루트노드에 있는지 find 하는 알고리즘은 U[7] = 4 ▷ U[4] = 2 ▷ U[2] = 2 (self number) 까지 올라가면 S2에 속해 있다는것을 알수 있게 되는것이다.
위 내용을 토대로 disjoint sets 의 union-find 자료구조를 구현해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
public class UF {
// disjoint sets의 무보노드 인덱스가 무엇인지 담을 공간
private int[] parent;
// 집합 (component 라고도함)의 개수를 나타냄(합집합을 하면 한개씩 줄어들 것이다.)
private int count;
/**
* 빈 서로수집합 자료구조를 UF 클래스를 초기화 한다.
* 처음에는 자기자신을 포함하고 있다,
*/
public UF(int n) {
if (n < 0) throw new IllegalArgumentException();
parent = new int[n];
count = n;
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
/**
* 해당 원소의 부모노드를 리턴하는 find 메소드.
* */
public int find(int p) {
validate(p);
while (p != parent[p]) {
p = parent[p];
}
return p;
}
/**
* 해당 원소 p, q 가 서로 연결되어 있는지, 즉 같은 집합에 포함되어 있으면 true, 그렇지 않으면 false
* 최소신장트리 생성시 사이클이 되어 있는지 확인하는 용도이기도 하다.
* */
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* p를 포함한 집합과 q를 포함한 집합의 합집합(merge)을 수행한다.
* */
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
count--;
}
private void validate(int p) {
int n = parent.length;
if (p < 0 || p >= n) {
throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
}
}
}
Colored by Color Scripter
|
Q. ★[DESIGN THINKING] ★ 이진트리의 WORST CASE 는 없는가 ? 예를들어 편향트리같은 ?
당연히 배열로 표현했지만 편향트리(skewed tree)가 발생할 수 있다.

처음 집합 10개인 것이 있을 때 다음과 같은 순서로 union 을 진행한다면 ? 오퍼레이션 수행할때마다 머릿속으로 그림을 그려보자.
union ( { 5 } , { 6 } );
union ( { 4 } , { 5, 6} );
union ( { 3 } , { 4, 5, 6} );
union ( { 2 } , { 3, 4, 5, 6} );
union ( { 1 } , { 2, 3, 4, 5, 6} );
union을 위처럼 수행하면 그림10 처럼 한쪽으로 편향된 트리가 구성된다.
이렇게 되면 find(6) 을 하게되면 총 6번의 비교를 해야만한다.
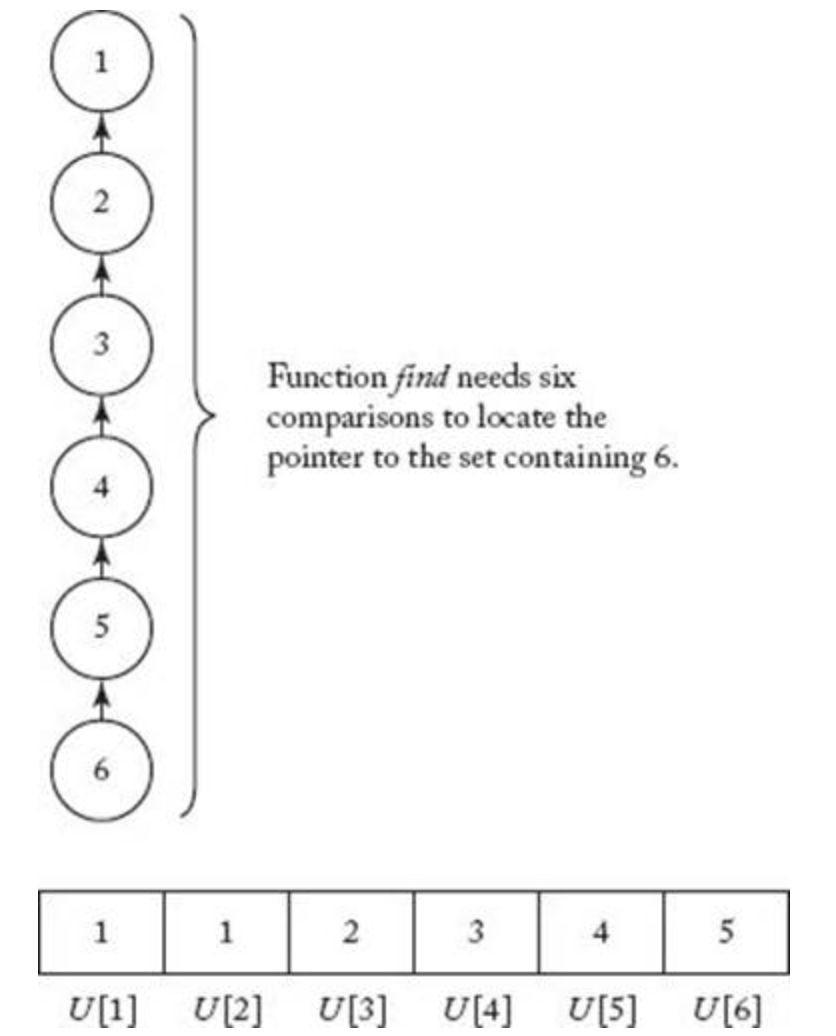
이진트리에서 높이의 균형을 마치기위해 균형이진트리 알고리즘류가 나온것처럼 이런 worst case가 나오지 않도록 할 방법은 없을까 ?
union시 기존 보다 최적화된 방법을 사용해야 하는데 좀만 생각해보면 답은 단순하다.
답은 union 시 둘 중 트리의 깊이가 더 작은 것을 다른 트리의 루트에 추가하는 것이다.
그림11 을 보면 상단은 기존의 방법처럼 한 것이고 하단은 둘 증 depth (깊이)가 작은 것을 깊이가 큰 거에 merge 하는 것이다.
기존처럼 했을 때는 depth 가 3이지만 새로운 방식은 2로 한단계 줄었다.
이 방식을 보통 union by rank 이라고 부른다.
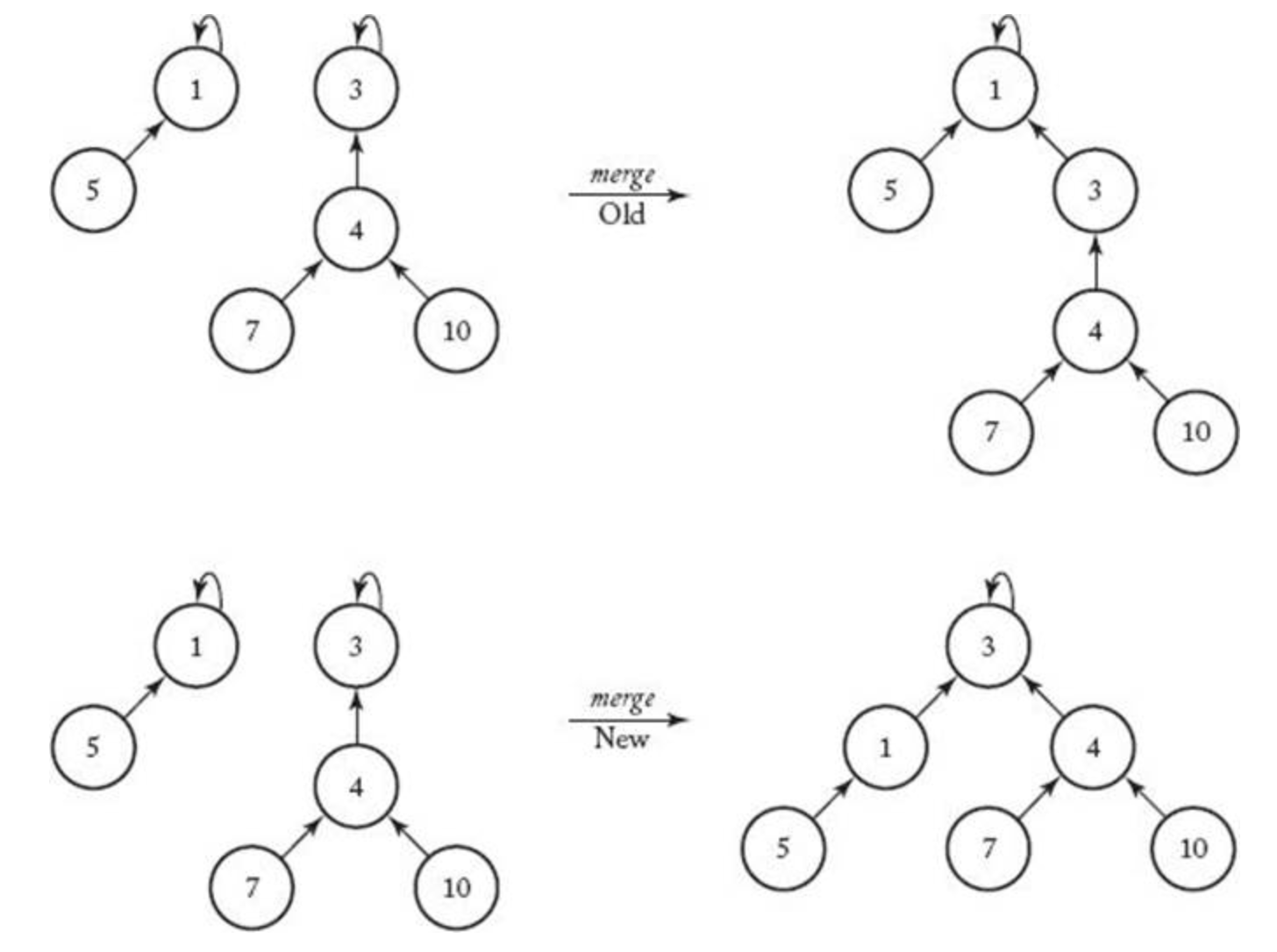
이 새로운 방식을 구현하려면 각 트리마다 depth를 기억하고 있다가 union시 둘중 작은 쪽을 큰 쪽으로 합치기만 하면된다.
아래 코드는 union by rank 방식을 이용하여 약간 수정한 버전이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
public class DisJointSetsUF {
// disjoint sets의 무보노드 인덱스가 무엇인지 담을 공간
private int[] parent;
private int[] rank;
// 집합 (component 라고도함)의 개수를 나타냄(합집합을 하면 한개씩 줄어들 것이다.)
private int count;
/**
* 빈 서로수집합 자료구조를 UF 클래스를 초기화 한다.
* 처음에는 자기자신을 포함하고 있다,
*/
public DisJointSetsUF(int n) {
if (n < 0) throw new IllegalArgumentException();
parent = new int[n];
rank = new int[n];
count = n;
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = i;
}
}
/**
* 해당 원소의 부모노드를 리턴하는 find 메소드.
* */
public int find(int p) {
validate(p);
while (p != parent[p]) {
p = parent[p];
}
return p;
}
/**
* 해당 원소 p, q 가 서로 연결되어 있는지, 즉 같은 집합에 포함되어 있으면 true, 그렇지 않으면 false
* 최소신장트리 생성시 사이클이 되어 있는지 확인하는 용도이기도 하다.
* */
public boolean connected(int p, int q) {
return find(p) == find(q);
}
/**
* p를 포함한 집합과 q를 포함한 집합의 합집합(merge)을 수행한다.
* */
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// make smaller root point to larger one
if (rank[rootP] < rank[rootQ]) {
parent[rootP] = rootQ;
rank[rootQ] += rank[rootP];
}
else {
parent[rootQ] = rootP;
rank[rootP] += rank[rootQ];
}
count--;
}
private void validate(int p) {
int n = parent.length;
if (p < 0 || p >= n) {
throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
}
}
}
Colored by Color Scripter
|
Q. 더 효율적인 방법은 ?
Rank and Path Compression 을 이용하는 방법이 있는데 있는데 이건 여기서 담에 시간나면 정리한다.
래퍼런스
- https://www.geeksforgeeks.org/union-find-algorithm-set-2-union-by-rank/
- https://algs4.cs.princeton.edu/15uf/
- https://apprize.info/science/algorithms/15.html
'자료구조(Data Structure)' 카테고리의 다른 글
| 방향그래프(Directed Graph) 구현 (0) | 2019.07.04 |
|---|---|
| 방향 비순환 그래프(DAG, Directed Acyclic Graph) (0) | 2019.07.04 |
| 무방향 그래프(Undirected Graph) 구현 (0) | 2019.07.03 |
| 그래프(Graph)란? (0) | 2019.07.03 |
| 자료구조(Data Structure)란 (0) | 2019.07.02 |


