그래프(Graph) 란 무엇인지 어느정도 확인을 하였는데 그럼 이런 G = (V,E)로 표현되는 그래프를 프로그래밍에서 어떻게 표현할수 있을까?를 고민해야 한다.
그래프를 프로그래밍에서 표현하기위한 방법은 크게 2가지 방법이 존재하는데 하나는 인접행렬(Adjacency matrix)이고 다른 하나는 인접리스트(Adjacency list)이다.
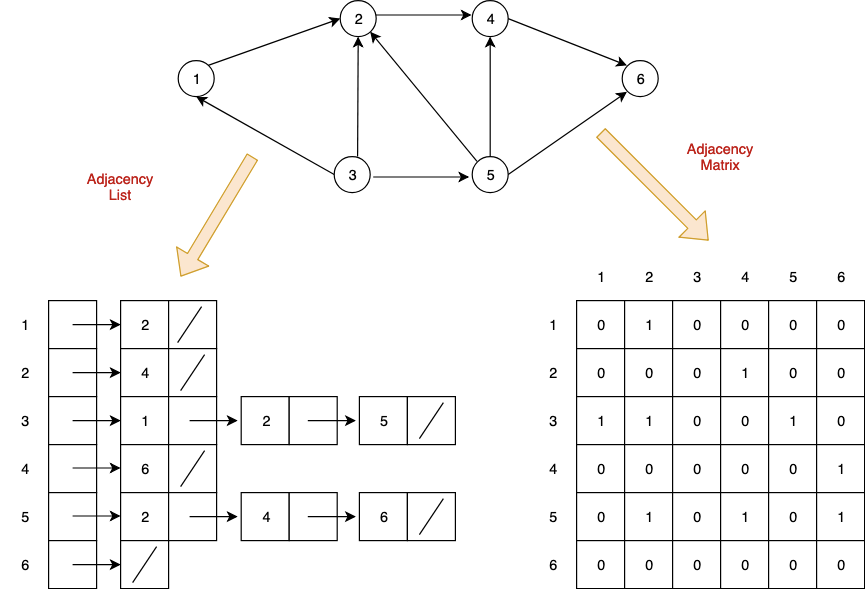
▲ [출처] https://algorithmtutor.com/Data-Structures/Graph/Graph-Representation-Adjacency-List-and-Matrix/
여기서는 2가지 모두 살펴볼것이고 인접행렬부터 알아보도록하자.
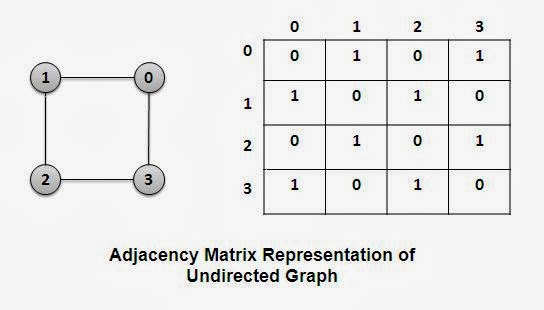
인접행렬의 사이즈 N 은 정점의 개수가 된다. V = { 0, ,1 ,2 3} 4개 이므로 사이즈 N * N = 4 * 4 가 된다.
행렬에서 가로, 세로축을 각각 i, j 라 할 때 정점끼리 연결된 에지는 1로 연결되지 않은것은 0으로 한다.
예를들어 정점 0 → 1이 서로 연결되어 있기 때문에 (i = 0 , j = 1) 위치에 1을 지정한다.
또한 무방향그래프는 방향이 없기 때문에 0 → 1 뿐만 아니라 1 → 0 도 연결되어 있음을 표현해야 한다.
따라서 (i = 0 , j = 1), (i = 1 , j = 0) 둘다 1로 지정 하면 된다.
방향그래프도 무방향그래프와 인접행렬로 표현하는 방식은 동일한데 차이점은 명확히 화살표가 가리키는 쪽만 1로 설정하는 것이다.
다음 그림은 0 → 1 방향으로 연결된 에지는 있지만 반대로 1 → 0 방향으로 연결된 에지는 없다. 무방향과는 다르다.
따라서 (i = 0 , j = 1) 위치만 1로 지정해야 하지 (i = 1 , j = 0) 를 1로 지정하면 안된다.

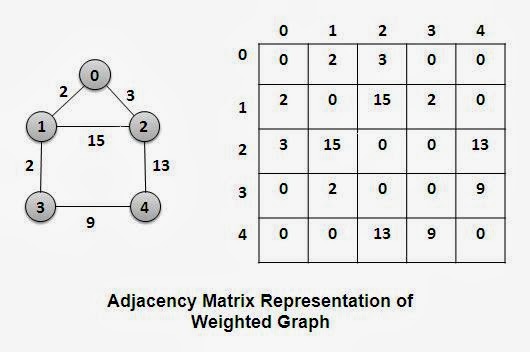
에지에 가중치가 있는 무방향그래프 or 에지에 가중치가 있는 방향그래프의 표현방식은 위에 살펴본것과 거의 동일한데 차이점은 1이 아닌 에지의 가중치를 행렬에 지정해야 해야 한다는 것이다.
아래 그림은 무방향 그래프이기 때문에 0 → 1 , 1 → 0 모두 에지로 연결되어 있고 (i = 0 , j = 1), (i = 1 , j = 0) 둘다 1로 지정해야 하지만
0 ↔ 1 에 가중치 2가 설정되어 있어 1이 아닌 2로 지정한 것이다.
인접행렬로 그래프를 표현하는 거는 구현 상 장단점이 있는데 어떤 정점 V 에 인접한(연결된) 모든 노드를 찾기위해서는 행 전체를 모두 검색(예를들어 0정점과 연결된 모든 정점을 찾기위해서는 0번 행이 1이상으로 지정되었는지 모두 탐색해야함) 해야 하기 때문에 O(n) 시간이 필요하지만 어떤 에지가 존재하는지 검사는 i,j 가 1 이상으로 지정되어 있는지 확인만 하면 되니 O(1)로 빠르다. 그리고 정점간 연결되지 않은 에지까지 N * N 에 표현 ( = 0 값으로) 되므로 저장공간이 낭비 ( O (n2) ) 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
|
import java.util.Iterator;
/**
* 인접 행렬을 이용한 그래프 구현.
* */
public class AdjMatrixGraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V ; // 정점(vertex)의 총 개수.
private int E ; // 에지(edge)의 총 개수
private boolean[][] adj; // 가중치가 없는 그래프라 boolean 으로 함.
public AdjMatrixGraph(int V) {
if (V < 0) throw new IllegalArgumentException("Too few vertices");
this.V = V;
this.E = 0;
// V * V 사이즈의 행렬(matrix)를 생성한다.
this.adj = new boolean[V][V];
}
// 정점의 개수를 리턴.
public int V() { return V; }
// 에지의 개수를 리턴.
public int E() { return E; }
// 정점간 에지를 추가한다.
public void addEdge(int v, int w) {
// 추가된적이 없으면 에지의 카운트를 +1
if(!adj[v][w])
E++;
adj[v][w] = true;
// 무방향 그래프이니 대칭행렬이 되도록 반대도 true 로 해준다.
adj[w][v] = true;
}
// 그래프에 v-w 에지가 있으면 true, 그렇치 않으면 false
// 행렬에서 [v][w]가 true 인지 , false 인지만 확인하면 되니 O(1) 이다.
public boolean contains(int v, int w) {
return adj[v][w];
}
// 정점 V와 인접한 리스트를 리턴한다.
public Iterable<Integer> adj(int v) {
return new AdjIterator(v);
}
private class AdjIterator implements Iterator<Integer>, Iterable<Integer> {
private int v;
private int w = 0;
AdjIterator(int v) {
this.v = v;
}
public Iterator<Integer> iterator() {
return this;
}
public boolean hasNext() {
while (w < V) {
if (adj[v][w]) return true;
w++;
}
return false;
}
public Integer next() {
if (!hasNext()) {
throw new NoSuchElementException();
}
return w++;
}
public void remove() {
throw new UnsupportedOperationException();
}
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " " + E + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (int w : adj(v)) {
s.append(w + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
}
Colored by Color Scripter
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public class Main {
public static void main(String[] args) {
AdjMatrixGraph graph = new AdjMatrixGraph(5);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
System.out.println(graph);
}
}
Colored by Color Scriptr
|
[출력]
5 7
0: 1 4
1: 0 2 3 4
2: 1 3
3: 1 2 4
4: 0 1 3
그래프를 인접리스트로 표현하기위해선느 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들을 연결리스트로 추가하면 된다. 아래 그림은 무바향 그래프를 인접리스트로 표현한 것인데 정점 V = { 0, 1, 2, 3, 4 } 5개가 있고 정점 집합을 표현하기위한 크기 5인 배열을 있다. 그리고 정점 0은 1, 2, 3,4, 정점과 에지로 연결되어 있기 때문에 E = { 0 ↔ 1, 0 ↔ 2, 0 ↔ 3, 0 ↔ 4 } 의 표현은 배열 index =0 에 연결리스트로 인접한 정점들의 목록을 추가하였고 무방향이기 때문에 반대에 대해서도 각각 연결리스트에 추가해주어야 한다.

인접리스트는 정점을 리스트로 연결하기 때문에 인접행렬보다 저장공간(메모리)면에서 더 효율적이다.
정점의개수가 n 이고 에지의 개수가 m 이라고 하면 무방향을 표현하기위해 연결된 리스트의 개수는 2m이 되어야 한다.
따라서 저장공간은 O(정점의개수+에지의개수*2) = O(n+m) 이 필요하고 어떤 정점 V에 인접한 모든 노드를 찾기위해서는 해당 정점의 배열에 있는 리스트를 모두 가져오면 되기 대문에 O(V 리스트의 개수) = O(degree(V)) 이고 어떤 에지 (U, V)가 존재하는지 검사하는 것은 O(degree(u)) 시간이 필요하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
|
import java.util.ArrayList;
import java.util.LinkedList;
/**
* 인접리스트를 사용해 그래프 구현.
* */
public class AdjListGraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V;
private int E;
private ArrayList<LinkedList<Integer>> adj;
public AdjListGraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
this.V = V;
this.E = 0;
// 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들을 연결리스트로 추가하기위한 연결리스트를 생성한다.
adj = new ArrayList<>(V);
for (int v = 0; v < V; v++) {
adj.add(new LinkedList<Integer>());
}
}
// 정점의 개수를 리턴.
public int V() {
return V;
}
// 에지의 개수를 리턴
public int E() {
return E;
}
// vertext 는 초기에 지정된 사이즈보다 크거나 0보다 작으면 안된다.
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
E++;
adj.get(v).add(w);
// 무방향 그래프이니 반대도 추가해야한다
adj.get(w).add(v);
}
// 정점의 인접리스트를 리턴한다.
public Iterable<Integer> adj(int v) {
validateVertex(v);
return adj.get(v);
}
// 정점과 연결된 인접리스트(edge) 개수를 리턴한다.
public int degree(int v) {
validateVertex(v);
return adj.get(v).size();
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
s.append(w + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
}
public class Main {
public static void main(String[] args) {
AdjMatrixGraph graph = new AdjMatrixGraph(5);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 3);
graph.addEdge(3, 4);
System.out.println(graph);
}
}
Colored by Color Scripter
|
레퍼런스
'자료구조(Data Structure)' 카테고리의 다른 글
| 방향그래프(Directed Graph) 구현 (0) | 2019.07.04 |
|---|---|
| 방향 비순환 그래프(DAG, Directed Acyclic Graph) (0) | 2019.07.04 |
| 그래프(Graph)란? (0) | 2019.07.03 |
| 자료구조(Data Structure)란 (0) | 2019.07.02 |
| 최소신장트리(Minimum Spanning Tree) (0) | 2019.07.02 |


