이진탐색트리(Binary Search Tree)

지금가지 트리(Tree)와 이진트리(Binary Tree)를 설명했다.

이번에 설명 할 이진탐색트리는 이진트리로 자료가 구성되는 트리중 하나인데 이진트리는와 다른점은 특정 규칙(rule)에 의해 자료가 저장되어 진다.

이전에 설명한 이진트리는 왼쪽 자식 노드(left node)와 오른쪽 자식 노드(right node)를 추가 할 때 추가될 데이터 정보와 상관없이 넣고 추가하고 싶은대로 추가하였다. 

사실 어떻게 보면 이진트리 모양을 만들기 위해 중구난방으로 자료를 추가했던 것이다.

이렇게 되면 자료의 탐색(or 검색)이 비효율적으로 된다.
자료를 탐색할 규칙이 없으니 당연히 복잡해지고 오래 걸리 수 밖에 없는 것이다.

반면 이진탐색트리는 이름에서 유추할 수 있듯이 탐색을 위한 트리 자료구조이라 자료 검색에 성능이 좋다.

 

도대체 어떤 방식으로 자료를 추가하길래 탐색성능이 좋을까?

이진탐색트리는 탐색을 위한 자료 구성을 위해 각 노드에 키값이 있다.

값들을 비교하여 추가, 삭제시 순서에 맞게 노드를 구성하는데 노드의 왼쪽 서브트리에는 그 노드의 키값 보다 작은 키값들을 지닌 노드들로 이루어져야 하고 노드의 오른쪽 서브트리에는 그 노드의 키값과  큰 키값들을 가진 노드들로 이루어져 있다.

left subtree (keys) < node (key) < right subtree (keys)

 

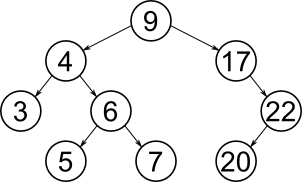
▲ [출처] https://www.chegg.com/homework-help/definitions/binary-search-tree-3

 

위 그림을 보면 각 노드에 숫자로 된 키가 있고 루트노드 = 9 를 기준으로 왼쪽 서브트리는 9보다 다 작은 값들이 있고, 오른쪽에서 9보다 다 큰값들이 있는것을 알수 있다.

또한 서브트리들을 보면 4를 가진 노드의 왼쪽은 4보다 작은 3이, 오른쪽 노드는 4보다 큰 6을 가진 노드가 있다. 

하나씩 노드를 보면 좌측은 상위 노드보다 작은값 우측은 동일하거나 큰 값으로 구성되어 있는것을 알수 있다.

이렇게 노드를 구성해 놓으면 평균적으로 O (log n)  성능으로 빠르게 탐색을 할 수 있는데   만약 7을 가진 노드를 찾고 싶다면 

아래와 같은 순서로 진행된다.

7을 가진 노드를 찾는 방법

① 키값이 9를 가진 노드와 비교한다.   7은 9보다 작기  때문에 왼쪽 서브트리에 있을 것이다.
② 4로 이동 되며 7을 4보다 크기 때문에 오른쪽 서브트리에 있을 것이다.
③ 6으로 이동 되며 7은 보다 크기 때문에 오른쪽으로 이동한다.
④ 마지막으로 해당 노드가 7을 가진값을 확인할 수 있다.

 

이진탐색트리는 이진트리와 구현이 거의 비슷한데  위에서 설명한 이진탐색트리의 특성을 만족하도록 변경하여 구현해보자.

우선 이진탐색트리의 BinarySearchTree 클래스와 노드를 나타내는 Node 클래스를 만들어보자

Node 클래스에는 왼쪽노드와 오른쪽노드를 참조하기위한 변수가 필요하다.

그리고 이진탐색트리는 키(key)값 비교(부모노의 키값보다 크냐 작으냐)를 통해 저장을 하기 때문에 비교하기 위한 키(key)가 필요하다. 

키(key)는 숫자일수도 있고 문자 or 문자열일수도 있고 비교 가능한(Comparable) 객체일수도 있다.

이진탐색트리는 그 종류에 따라 키(key)만 있는 경우도 있고 키에 해당하는 값=데이터(value)을 가질수도 있다. 

어찌 보면 Set vs HashTable (or HashMap) 차이라고 보면되는데 키값이 데이터인 경우와  키에 매칭되는 값이 따로 있는 경우도 있을수 있다. 여기서는 후자를 고려해서 구현할 것이다.

 

// Key 값은 비교 가능해야하니 Comparable 를 상속한 클래스이어야 한다.
public class BinarySearchTree<Key extends Comparable<Key>, Value> {
    
    public Node root ;  // 이진탐색트리의 루트 노드
 
    public class Node {
        public Key key    ; // 노드의 키값이고 이거에 의해 정렬되어 질 것이다.
        public Value val  ; // 노드의 값.
        private Node left  ; // 왼쪽 서브트리 노드, 
        private Node right ; // 오른쪽 서브트리 
        private int size   ; // 서브트리 노드의 개수.
 
        public Node(Key key, Value val, int size) {
            this.key = key;
            this.val = val;
            this.size = size;
        }
    }
}

 

Node 를 추가(put) 할때 해당 키값을 root 노드 부터 비교하여(compare) 작으면 왼쪽으로 크면 오른쪽으로 이진트리의 특성을 만족 할 때까지 하위 서브트리까지 내려가면서 위치를 찾아 추가하면 된다. 만약 해당 키값이 이미 추가되어 있다면 값만 업데이트 해주면 된다.

 

public void put(Key key, Value val) {
    if (key == null) throw new IllegalArgumentException("calls put() with a null key");
    root = put(root, key, val);
 
}
 
private Node put(Node x, Key key, Value val) {
    // 만약 x 가 null 이면 root 노드를 생성하여 리턴한다.
    if (x == null) {
        return new Node(key, val);
    }
 
    // 현재 노드와 키를 비교하여 작으면 왼쪽 노드, 크면 오른쪽 노드에 추가해준다.
    // 조건이 만족할때까지 서브트리를 검색해야 하므로 재귀방식으로 호출한다.
    int cmp = key.compareTo(x.key);
    if (cmp < 0) {
        x.left = put(x.left, key, val);
    }
    else if (cmp > 0) {
        x.right = put(x.right, key, val);
    }
    else {
        // 키값이 같으면 이미 추가된 것이고 값만 업데이트 해준다.
        x.val = val;
    }
 
    return x;
}

 

추가한 자료를 검색하기위한 방법은 추가할때 했더 순서대로 검색해 나가면 된다.

먼저 루트노드 부터 키값을 비교한다. 키값이 같으면 바로 리턴하고 그렇지 않고 노드 키값보다 작다면 왼쪽 서브트리를 , 노드 키값보다 크다면 오른쪽서브트리를 재귀적으로 검색하면서 키값이 같은지 비교하면 된다.

 

// 키가 존재한다면 true 를 그렇치 않다면 false 를 리턴한다.
public boolean contains(Key key) {
    if (key == null) throw new IllegalArgumentException("argument to contains() is null");
    return get(key) != null;
}
 
// 키가 존재한다면 키에 대한 값을 리턴한다. 
public Value get(Key key) {
    return get(root, key);
}
 
// 키를 검색하기위한 상세 구현 함수
private Value get(Node x, Key key) {
    if (key == null) throw new IllegalArgumentException("calls get() with a null key");
 
    // 재귀함수의 base case 임.
    if (x == null) return null;
 
    int cmp = key.compareTo(x.key);
    // 키값이  작다면 왼쪽 서브트리 검색
    if (cmp < 0) {
        return get(x.left, key);
    }
    // 키값이 크다면 오른족 서브트리 검색
    else if (cmp > 0) {
        return get(x.right, key);
    }
    // 키값이 가다면 리턴.
    else {
        return x.val;
    }
}

 

 

마지막으로 자료 순회를 위한 4가지 방법 ( pre-order, in-order, post-order, level-order) 을 구현해보자.

트리 자료 순회에 대해 잘 모른다면 트리(Tree)와 이진트리(Binary Tree) 를 먼저 읽고 오기 바란다.

 

public void preorderTraversal(Node node, Consumer < Node > consumer) {
    if (node == null) return;
 
    // root -> left -> right
    if (consumer != null) consumer.accept(node);
    preorderTraversal(node.left, consumer);
    preorderTraversal(node.right, consumer);
}
 
public void inorderTraversal(Node node, Consumer < Node > consumer) {
    if (node == null) return;
 
    // left -> root -> right
    inorderTraversal(node.left, consumer);
    if (consumer != null) consumer.accept(node);
    inorderTraversal(node.right, consumer);
}
 
public void postorderTraversal(Node node, Consumer < Node > consumer) {
    if (node == null) return;
 
    // left -> right -> root
    postorderTraversal(node.left, consumer);
    postorderTraversal(node.right, consumer);
    if (consumer != null) consumer.accept(node);
}
 
public void levelOrderTraversal(Node root, Consumer < Node > consumer) {
 
    final Queue < Node > queue = new ArrayDeque < >();
    queue.add(root);
 
    while (!queue.isEmpty()) {
        Node node = queue.poll();
        consumer.accept(node);
        if (node.left != null) queue.add(node.left);
        if (node.right != null) queue.add(node.right);
 
    }
}

 

여기 까지 구현된것이 잘 되는지 데이터 구성을 다음 그림처럼 하고 테스트 해본다.

 

 

 
public class Main {
 
    public static void main(String[] args) throws IOException {
 
        // 키를 값으로 하는 BST라 키,값이 integer, integer 이다.
        BinarySearchTree<Integer, Integer> bst = new BinarySearchTree<>();
 
        int []keys = { 9, 4, 17, 3, 6, 5, 7, 22, 20 };
        for(int i = 0 ; i < keys.length ; i++) {
            bst.put(Integer.valueOf(keys[i]), Integer.valueOf(keys[i]));
        }
 
        // 이진탐색트리에서 해당 키를 검색해본다.
        // 10과 8은 없기 대문에 false 를 리턴해야 한다.
        int []searchKeys = { 9, 4, 10, 3, 6, 8, 7, 22, 20 };
        for(int i = 0 ; i < searchKeys.length ; i++) {
            boolean ret = bst.contains(Integer.valueOf(searchKeys[i]));
            System.out.println(String.format("key = %d, exist = %s",
                    searchKeys[i], ret == true ? "true" : "false"));
        }
 
 
        // 트리를 순회한다.
        System.out.println("pre-order");
        bst.preorderTraversal(bst.root, (node) -> System.out.print(node.key + " ,"));
 
        System.out.println("\nin-order");
        bst.inorderTraversal(bst.root, (node) -> System.out.print(node.key+ " ,"));
 
        System.out.println("\npost-order");
        bst.postorderTraversal(bst.root, (node) -> System.out.print(node.key+ " ,"));
 
        System.out.println("\nlevel-order");
        bst.levelOrderTraversal(bst.root, (node) -> System.out.print(node.key+ " ,"));
    }
    
}

Note - preorder -> 이진탐색트리생성 방법

만약 preorder sequence 가 { 10, 5, 1, 7, 40, 50 } 가 되어 있다면

1.  preorder 순서 중 첫번째 키는 항상 이진트리의 루트(root) 노드이기 때문에 루트노드를 생성 한다. (ex. 10 이 루트노드가 된다.)
2. 그 다음에 루트 노드 보다 큰 키값을 가진 첫 번째 요소를의 인덱스 i 를 찾는다. ( ex. 여기서는 40 이 루트노드 10보다 큰 값을 가진 것중 가장 첫번째 요소이다. )
3. 루트노드를 제외한 i 이전 까지의 키들은 왼쪽 서브트리(left subtree)가 되고 ( ex. left subtree ∈ { 5, 1, 7 } )
4. i 를 포함하여 i 이후의 모든 키들은 오른쪽 서브트리(right subtree)가 된다.  ( ex. right subtree ∈  {40, 50} )
5. 1-4번을 재귀적으로 반복한다.   

public static Node buildNodeFromPreOrder(Key[] preorder, int start, int end) {
    // base case
    if (start > end) {
        return null;
    }
    Node node = new Node(preorder[start], null);
    int i = start;
    while (i <= end) {
        if (preorder[i].compareTo(node.key) > 0) {
            break;
        }
        i++;
    }
    node.left = buildNodeFromPreOrder(preorder, start + 1, i - 1);
    node.right = buildNodeFromPreOrder(preorder, i, end);
    return node;
}