이진트리(Binary Tree)와 이진탐색트리(Binary Search Tree)차이가 노드 추가시 노드의 왼쪽 서브트리에는 그 노드의 키값 보다 작은 값들이 오른쪽 서브트리는 노드의 키값보다 큰 값들이 와야하는 규칙이 있었던 것처럼 힙도 이진트리 중 -> 완전이진트리(complete binary tree)로 노드가 구성되어야 하고 노드 추가시 몇 가지 규칙이 있다.
완전이진트리(complete binary tree)란 마지막 레벨을 제외한 나머지 노드가 꽉 차 있어야 하며(마지막 레벨을 제외하고 포화이진트리이어야 하며), 마지막 레벨의 노드는 왼쪽 부터 차있어야 한다고 이진트리(Binary Tree)에서 설명한 적이 있다.

원래 힙은 데이터 원소 중에서 최대값(MAX) 및 최소값(MIN)을 찾아내는 연산을 빠르게 하기 위해 고안된 것인데 우선순위큐(Priority Queue), 힙정렬(Heap Sort), 압축 알고리즘인 허프만 코드(Huffman Code) 에도 응용되기 때문에 잘 알아 두어야 한다.
힙은 부모노드의 값이 자식노드의 값과 비교하여 부모노드가 큰 순서대로 저장되느냐 작은 순서대로 저장되느냐에 따라 2가지 타입으로 나누어 지는데 부모노드가 큰 순서대로 저장되는 것을 최대힙(Max Heap) 이라 하고 부모노드가 작은 순서대로 저장되는 것을 최소힙(Min Heap)이라 한다.
그럼 최소힙, 최대힙을 구성하기위한 rule 은 무엇인지 알아보자.
아래 그림은 부모 노드의 키값이 자식도드보다 항상 작은 값을 가지도록 구성된 최소힙을 보여주고있는데
루트노드 10은 자식인 왼쪽자식인 14보다 작고 오른쪽자식노드인 19보다도 작다.
또한 왼쪽서브트리도 마자찬가지인데 14를 가진 노드는 왼쪽자식인 26보다 작고 오른쪽자식노드인 31보다 작으로 오른쪽 서브트리도 마찬가지이다.
키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않다는것을 유념해야한다.
각 노드의 자식노드의 최대개수는 힙의 종류에 따라 다르지만, 대부분의 경우는 자식노드의 개수가 최대 2개인 이진 힙(binary heap)을 사용하고 루트노드에 항상 데이터들 중 가장 작은 값이 저장되어 있기 때문에, 최소값을 O(1) 안에 찾을 수 있고 데이터의 삽입과 삭제는 모두 O(log N)이 소요된는 특성을 가지고 있다.

▲[출처] https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm
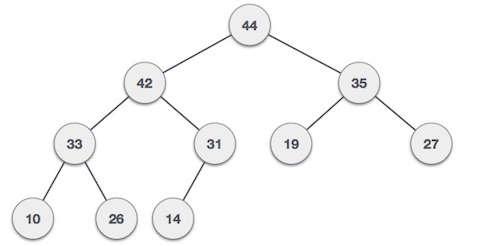
아래 그림은 부모 노드의 키값이 자식도드보다 항상 큰 값을 가지도록 구성된 최대힙을 보여주고있는데
루트노드 44은 자식인 왼쪽자식인 42보다 크고 오른쪽자식노드인 35보다도 크다.
또한 왼쪽서브트리도 마자찬가지인데 42를 가진 노드는 왼쪽자식인 33보다 크고 오른쪽자식노드인 31보다 크며, 오른쪽 서브트리도 마찬가지이다.
최소힙과 마찬가지로 키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않다는것을 유념해야한다.
각 노드의 자식노드의 최대개수는 힙의 종류에 따라 다르지만, 대부분의 경우는 자식노드의 개수가 최대 2개인 이진 힙(binary heap)을 사용하고 루트노드에 항상 데이터들 중 가장 작은 값이 저장되어 있기 때문에, 최대값을 O(1) 안에 찾을 수 있고 데이터의 삽입과 삭제는 모두 O(log N)이 소요된는 특성을 가지고 있다.
▲[출처] https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm

▲[출처] https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm
힙의 속성에 맞게 데이터를 추가하기 위한 알고리즘은 다음과 같다.
2. 끝에 추가된 노드에 키값(value)을 할당(assign) 한다.
3. 노드의 키값과 부모노드의 키값을 비교한다.
4. 노드의 키값이 부모노드의 키값보다 크다면 그것을 서로 스왑(swap) 한다.
5. 힙 속성이 유지 될 때까지 3, 4 단계를 반복한다.
위 그림에서 최대힙 노드 추가시 각 노드들이 최대힙 속성을 유지하기위해 내부적으로 어떤 과정을 거치는지 애니매이션을 보여주고 있는데 살펴본 알고리즘에 맞게 노드가 추가되는것을 확인할 수 있을 것이다.

▲[출처] https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm
2. 마지막 레벨의 마지막 노드를 (즉, 힙의 맨 끝에 있는 노드) 루트노드로 이동한다.
3. 루트 노드의 키값과 자식노드의 키값을 비교한다.
4. 루트의 키값이 자식노드의 키값보다 작다면 그것을 서로 스왑(swap) 한다.
5. 힙 속성이 유지 될 때까지 3, 4 단계를 반복한다.
위 그림에서 최대힙 노드 삭제시 각 노드들이 최대힙 속성을 유지하기위해 내부적으로 어떤 과정을 거치는지 애니매이션을 보여주고 있는데 살펴본 알고리즘에 맞게 노드가 삭제되고 있는것을 확인할 수 있을 것이다.
힙 자료구조 속성을 모두 알아 보았으니 구현을 해보자.
힙은 이진트리(완전이진트리)를 기반으로 하기 때문에 이진트리(Binary Tree) 에서 사용했던 포인터(참조)로 노드를 구현하는 방법을 사용해도 상관없지만 원래 이지트리는 포인터가 아닌 배열로도 구현이 가능하다.
배열로 구현 가능한 이유는 다음과 같은 이진트리 특성 때문이다.

▲ [출처] http://faculty.washington.edu/jstraub/dsa/slides/09Binary%20Trees/140BinaryTreeArray.html
예를들어 inx=3인 D노드의 부모노드 인덱스는 (3-1)/2 = 1 이 되고 inx=1 인 B를 가리키고 있다.
2. 노드 왼쪽자식노드는의 배열 인덱스는 (2 * (inx) + 1) 이 된다.
예를들어 루트노드 A의 inx=0 의 왼쪽자식노드는 B (inx = 1) 인데 위 공식에 대입하면 (2 * (0) + 1) = 1 과 정확히 일치한다.
3. 노드 오른쪽자식노드의 배열 인덱스는 (2 * (inx) - 2) 이 되다.
예를들어 루트노드 A의 inx=0 의 왼쪽자식노드는 C (inx = 2) 인데 위 공식에 대입하면 (2 * (2) + 2) = 2 와 정확히 일치한다는 것을 알수 있다.
자 이제 힙의 속성과 이진트리를 배열로 구성할 수 있음을 알게되었으니 최소힙과 최대힙을 배열로 구현하도록 해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
import java.util.Comparator;
public class Heap<Key> {
// 이진힙을 구성 할 때 노드를 포인터(참조)로 연겷지 않고 배열에 저장하기 위한 변수
private Object[] nodes;
// 최대힙, 최소힙에서 부모와 자식간의 키값 비교를 위한 Comparator 변수
private Comparator<? super Key> comparator;
// 힙에 맨 마지막노드(terminal node)가 저장된 배열의 index
private int last = -1;
/**
* @param comparator 부모 자식간의 키값 비교를 위한것으로 최대힙으로 정렬할지 최소힙으로 정렬할지 결정할수 있다.
* */
public Heap( Comparator<? super Key> comparator) {
this.nodes = new Object[16];
this.comparator = comparator;
}
// 힙에 자료를 추가한다. 데이터 추가 알고리즘을 참고할 것.
public boolean offer(Key x) {
if (x == null)
throw new NullPointerException();
// 1. 힙의 끝에 새로운 노드를 생성한다
// 2. 끝에 추가된 노드에 키값(value)을 할당(assign) 한다.
last += 1;
nodes[last] = x;
// 3. 노드의 키값과 부모노드의 키값을 비교한다.
int k = last;
while (k > 0) {
int parent = (k - 1)/2;
Object e = nodes[parent];
if (comparator.compare(x, (Key) e) >= 0)
break;
// 4. 노드의 키와 부모노드의 키를 비교하여 스왑(swap)이 필요한경우 swap 한다.
nodes[k] = e;
k = parent;
}
nodes[k] = x;
return true;
}
// 힙에 자료를 제거한다.
public Key poll() {
if (last == -1)
return null;
// 1.루트노드를 제거한다.
// 2.마지막 레벨의 마지막 노드를 (즉, 힙의 맨 끝에 있는 노드) 루트노드로 이동한다.
Key result = (Key) nodes[0];
Key x = (Key) nodes[last];
nodes[last] = null;
nodes[0] = x;
--last;
// 3. 루트 노드의 키값과 자식노드의 키값을 비교한다.
int k = 0;
int half = (last+1) >>> 1;
while (k < half) {
int child = (k << 1) + 1; // 왼쪽자식차일드.
Object c = nodes[child];
int right = child + 1; // 오른쪽자식노드
// 4. 노드의 키와 부모노드의 키를 비교하여 스왑(swap)이 필요한경우 swap 한다.
// 왼쪽, 오른쪽 비교하여 둘중에 오른쪽서브트리로 결정해야하는 경우임.
if (right <= last && comparator.compare((Key) c, (Key) nodes[right]) > 0)
c = nodes[child = right];
if (comparator.compare(x, (Key) c) <= 0)
break;
nodes[k] = c;
k = child;
}
nodes[k] = x;
return result;
}
}
Colored by Color Scripter
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class Main {
public static void main(String[] args) {
Heap<Integer> heap= new Heap<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2; // 최소힙을 위해 오름 차순.
}
});
heap.offer(35);
heap.offer(33);
heap.offer(42);
heap.offer(10);
heap.offer(14);
heap.offer(19);
heap.offer(27);
heap.offer(44);
heap.offer(26);
heap.offer(31);
Integer i = heap.poll();
while(i != null) {
// 출력 10, 14, 19, 26, 27, 31, 33, 35, 42, 44
System.out.println(i);
i = heap.poll();
}
}
}
Colored by Color Scripter
|
'자료구조(Data Structure)' 카테고리의 다른 글
| 이진트리(Binary Tree) (0) | 2019.06.18 |
|---|---|
| 우선순위큐(Priority Queue) (0) | 2019.06.18 |
| 트리(Tree) (0) | 2019.06.18 |
| 스택(Stack) (0) | 2019.06.18 |
| 큐(Queue) (0) | 2019.06.18 |



