트리(Tree) POST에서는는 자식노드의 개수에 상관없이 계층적으로 구성되어 있는것을 구현해보았다.
이런 트리중 좀 특별한게 있는데 바로 이진트리(Binary Tree)이다.
이진트리란 노드가 최대 2개이하의 자식노드를 가지는 트리 자료구조로 자식노드는 각각 왼쪽 자식 노드(left child node)와 오른쪽 자식 노드 (right child node)로 구성된다.

▲[출처] https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm
위 그림은 A 노드는 왼쪽에 B노드 오른쪽에 C 노드를 자식으로 가지고 있으며 B노드는 왼쪽에 D노드를 오른쪽에 E노드를 자식으로 가지고 있고 모든 노드의 자식노드는 2개이하로 구성되어 있는 이진트리이다.
왜 이렇게 이진트리라는것이 필요할까? 궁금할텐데 보통 이진트리는 자료의 검색과 탐색 [ex. 이진탐색트리(Binary Search Tree) ] or 상태공간트리를 구성하는데 있어 효율적이기 때문이다.
이진트리는 자식노드가 어떻게 구성되어 있냐에 따라 다음과 같이 5가지로 구분된다.
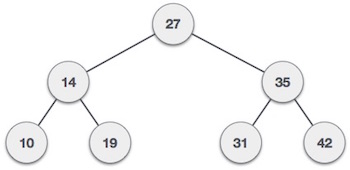
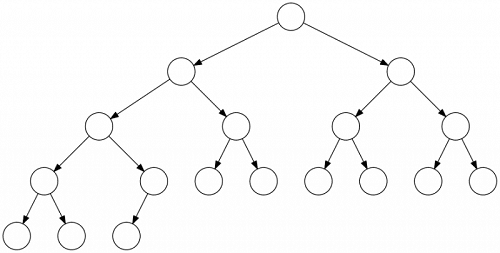
▣ 정 이진 트리(full binary tree) or Strictly binary tree : 트리의 모든 노드가 0개 혹은 2개의 자식을 가지는 경우이다. 즉 자식을 하나만 가진 노드가 없어야 한다. 완전이진트리는 자식을 1개만 가질수도 있고 포화이진트리는 모든레벨이 2개자식을 가져야 하므로 정 이진트리와 다르다. 아래 왼쪽 그림은 C 노드가 H 한개만 자식노드를 가지기 때문에 정이진트리가 될 수 없으나 오른쪽 트리는 모든 노드가 0개 또는 2개의 자식노드를 가지고 있으므로 정이진트리이다.

▲[출처] https://www.gatevidyalay.com/binary-tree-types-of-trees-in-data-structure/
편향 이진 트리는 검색에 성능 이슈가 있는데 이런 문제점을 극복하기위해 AVL트리 , 레드-블랙트리(Red-Black Tree)같은 변종이 생겨났다. 이건 다른 POST에서 좀더 자세히 다룬다.
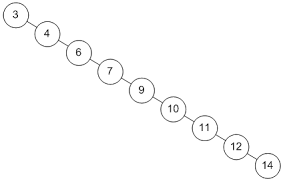
▣ 균형이진트리 (balanced binary tree) : 트리에 삽입과 삭제가 일어나는 경우에 자동으로 그 높이(루트에서부터 내려갈 수 있는 최대 레벨)를 작게 유지하는 노드기반 이진 탐색 트리이다.
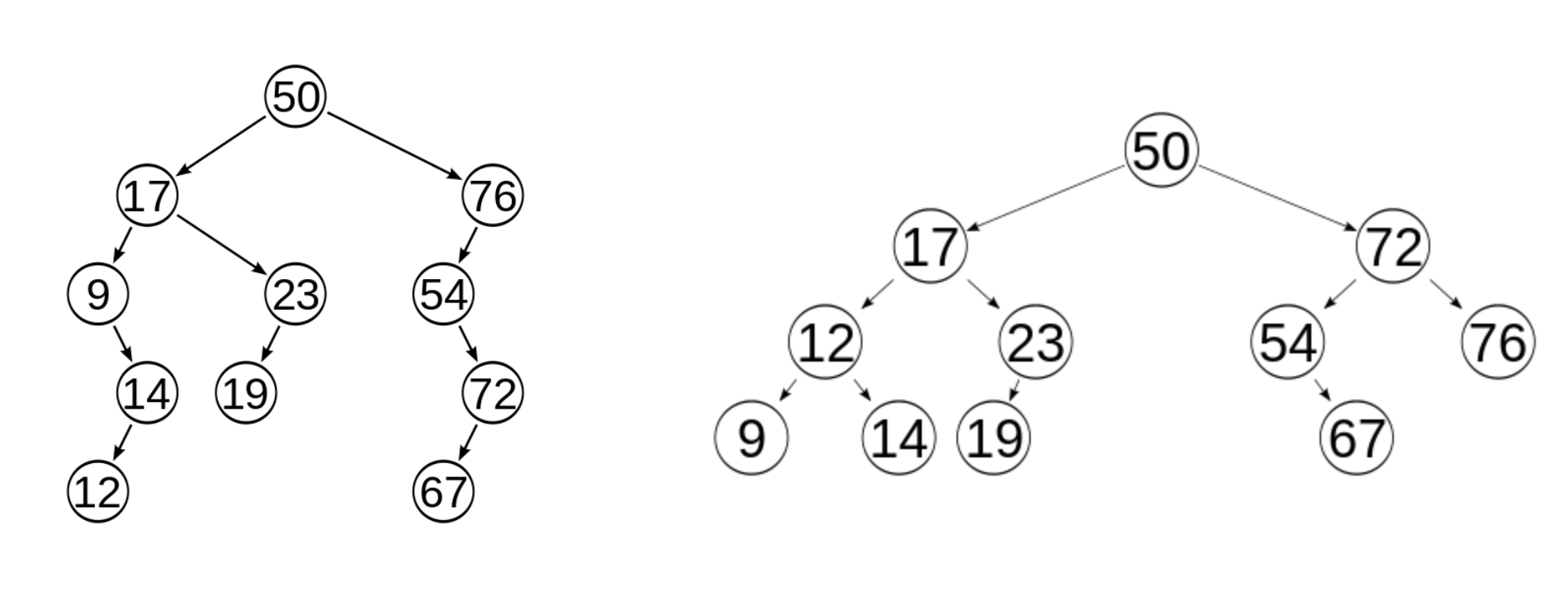
아래 왼쪽트리는 균형이 맞지 않는(unbalanced) 트리의 예로 루트에서 특정 노드로 갈 때, 평균 3.27회의 노드 접근이 필요하다.
하지만 오른쪽 트리는 동일하 자료를 유지하면서 트리를 높이 균형을 맞춘 후의 상태(균형이진트리상태) 로 평균 이동 비용이 3.00 노드 접근(node access)로 감소되것을 알 수 있다.
자세한 것은 AVL트리 , 레드-블랙트리(Red-Black Tree) POST에서 설명하겠다.
이진트리가 어떻게 생겼는지 이제 알았으니 코드로 이진트리를 구현해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public class BinaryTree<T> {
public static class Node<T> {
public T data ; // 노드의 값.
public Node<T> parent ; // 부모 노드를 가리킨다.
public Node<T> left ; // 왼쪽 자식노드 (left child node)
public Node<T> right ; // 오른쪽 자식노드(right child node)
Node(T data) {
this.data = data;
}
public Node(Node<T> parent, T data ) {
this.data = data;
this.parent = parent;
this.left = null;
this.right = null;
}
}
public Node addLeft(Node parent, T data) {
Node node = new Node(parent, data);
parent.left = node;
return node;
}
public Node addRight(Node parent, T data) {
Node node = new Node(parent, data);
parent.right = node;
return node;
}
}
Colored by Color Scripter
|
이진트리 클래스를 사용하여 아래 그림처럼 트리를 구성해보자

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public class Main {
public static void main(String[] args) {
BinaryTree<String> binaryTree = new BinaryTree();
binaryTree.addLeft(bNode, "D");
binaryTree.addRight(bNode, "E");
binaryTree.addLeft(cNode, "F");
binaryTree.addRight(cNode, "G");
}
}
Colored by Color Scripter
|
이진트리를 구성하였으면 트리에 있는 모든 목록을 탐색 or 순회(traversal or iteration) 할 수 있어야 한다.
모든 자료구조는 순회필수이다. 근데 트리는 순회하는 방법이 보통 3가지(preorder, inorder, postorder)가 있다.
레벨순회(level traversal)도 있는데 이건 트리(Tree) 포스트를 참고하면 된다.
▣ 전위 순회(preorder traversal) : V(루트방문) -> L(왼쪽서브트리방문) -> R(오른쪽서브트린방문) 순으로 순회한다.
아래 이미지를 기준으로 설명하면 처음 A 루트노드를 방문하고 그다음 왼쪽 서브트리 B를 다시 preorder 로 순회한다.
왼쪽 서브트리가 끝나면 오른쪽 서브트리 C를 다시 predoer 로 순회하게 된다.
그럼 순서는 A → B → D → E → C → F → G 로 순회하게 된다.

|
1
2
3
4
5
6
7
8
9
|
if(node == null)
return;
preorderTraversal(node.left, consumer);
preorderTraversal(node.right, consumer);
}
Colored by Color Scripter
|
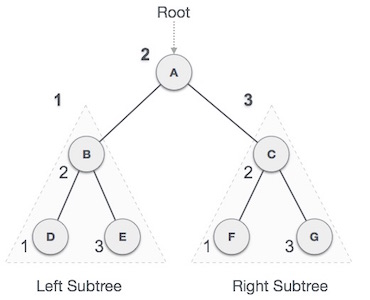
▣ 중위 순회(inorder traversal) : L(좌측서브트리방문) -> V(루트노드방문) -> R(우측서브트리방문) 순으로 순회한다.
처음 좌측 서브트리 B를 in-order 로 순회한다. B 서브트리가 끝나면 이제 루트로 이동하게 되고 루트방문이 끝나면 우측 C 서브트리를 in-order로 순회하게 된다.
그럼 순서는 D → B → E → A → F → C → G 로 순회하게 된다.
|
1
2
3
4
5
6
7
8
9
|
if(node == null)
return;
// left -> root -> right
inorderTraversal(node.left, consumer);
inorderTraversal(node.right, consumer);
}
Colored by Color Scripter
|
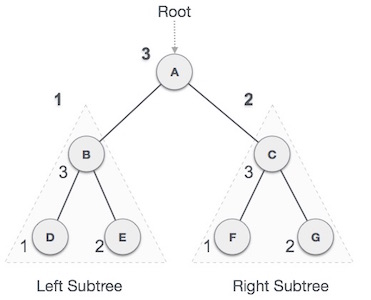
▣ 후휘 순회(postorder traversal) : L(좌측서브트리방문) -> R(우측서브트리방문) -> V(루트방문) 순으로 순회한다.
B서브트리를 postorder 로 순회한다. 그리고 우측서브트리인 C 를 postorder로 순회하고 마지막으로 A인 루트노드를 방문하면서 끝난다.
그럼 순서는 D → E → B → F → G → C → A 로 순회하게 된다.
|
1
2
3
4
5
6
7
8
9
10
|
if(node == null)
return;
// left -> right -> root
postorderTraversal(node.left, consumer);
postorderTraversal(node.right, consumer);
}
Colored by Color Scripter
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class Main {
public static void main(String[] args) {
BinaryTree<String> binaryTree = new BinaryTree();
binaryTree.addLeft(bNode, "D");
binaryTree.addRight(bNode, "E");
binaryTree.addLeft(cNode, "F");
binaryTree.addRight(cNode, "G");
final StringBuilder builder = new StringBuilder("preorder : ");
binaryTree.preorderTraversal(root,
builder.append("\n");
builder.append("inorder : ");
binaryTree.inorderTraversal(root,
builder.append("\n");
builder.append("postorder : ");
binaryTree.postorderTraversal(root,
System.out.println(builder.toString());
}
}
Colored by Color Scripter
|
코드를 실행하면 출력은 아래와 같다. 각 라인마다 맨 뒤에 -> 를 빼고 싶었으나 귀찮아서 빼지 않았다.
preorder : A->B->D->E->C->F->G->
inorder : D->B->E->A->F->C->G->
postorder : D->E->B->F->G->C->A->
'자료구조(Data Structure)' 카테고리의 다른 글
| 덱(Deque) (0) | 2019.06.18 |
|---|---|
| 이진탐색트리(Binary Search Tree) (0) | 2019.06.18 |
| 우선순위큐(Priority Queue) (0) | 2019.06.18 |
| 힙(Heap) (0) | 2019.06.18 |
| 트리(Tree) (0) | 2019.06.18 |



