분할정복 알고리즘(Divide and Conquer Algorithm)이란 해결하고자 하는 문제(Problem)를 통째로 놓고 푸는 것이 아니고 문제를 작은 크기의 동일한 문제들(Problems)로 분할해서 각각의 작은 문제를 순환적으로 해결하는 방법을 말한다.
▲ [출처] https://medium.com/cracking-the-data-science-interview/divide-and-conquer-algorithms-b135681d08fc
분할정복에 대한 유례는 1805년 12월 2일 아우스터리츠 전투에서 프랑스의 황제 나폴레옹이 사용했던 훌륭한 전략에서 따왔다고 한다.
오스트리아-러시아 연합군은 나폴레옹의 군대보다 15,000명 정도 많았다.
연합군은 프랑스군의 우측면에 대규모 공격을 감행했다. 공격을 예상한 나폴레옹은 연합군의 중앙으로 쳐들어가, 그들의 병력을 둘로 갈라 놓았다. 둘로 나눠진 병력은 개별적으로는 나폴레옹의 군대와 상대가 되지 못했기 때문에, 패하고 퇴각하지 않을 수 없었다.
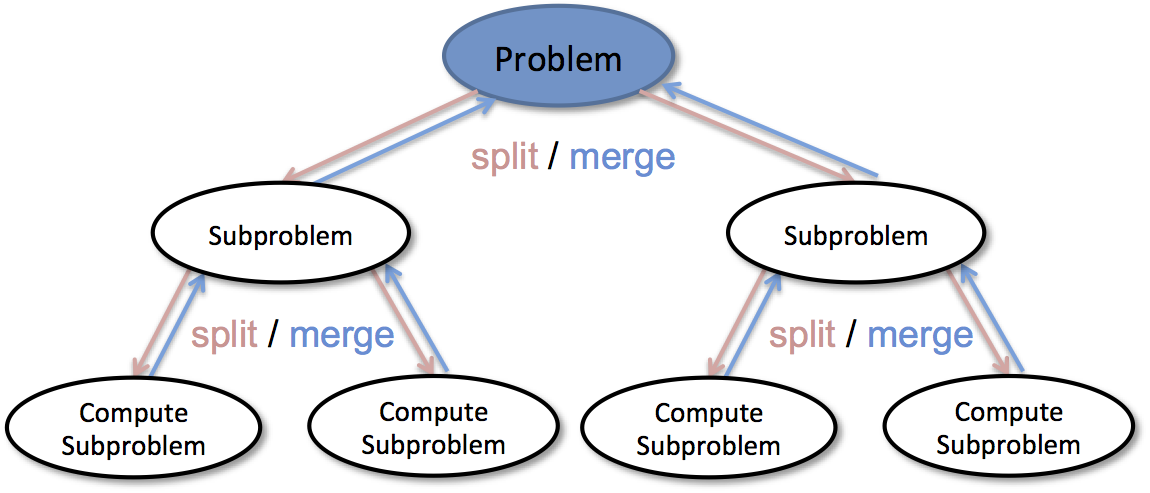
분할정복법은 위와 같은 사례를 적극 이용한다. 문제의 사례를 2개 이상의 더 작은 사례로 나눈다. 이 작은 사례는 주로 원래 문제에서 따온다. 나눈 작은 사례의 해답을 바로 얻을 수 있으면 해를 구하고 아니면 더 작은 사례로 나눈다.
이처럼 해를 구할 수 있을 만큼 충분히 더 작은 사례로 나누어 해결하는 방법이다.
[출처 : http://www.seehint.com/word.asp?no=12188]
이런 분할 정복 알고리즘을 사용하여 문제를 해결하는 대표적인 알고리즘에는 퀵정렬(Quick Sort)나 합병정렬(Merge Sort)같은 정렬 알고리즘이나 이진탐색(Binary Search) 고속푸리에변환(Fast Fourier Transform : FFT) 에 사용되기도하고 요즘 트렌드인 빅데이터를 분석 할 때 하나의 머신(Machine)에서 많은 데이터를 분석하지 않고 데이터를 쪼개서 여러 머신에서 처리하도록 한 다음(병렬처리) 그 결과를 합쳐( Merge) 최종적으로 리포팅하여 시간을 절약하는 방법도 일종의 분할 정복이라고 볼수 있다.
분할정복과 동적프로그래밍(Dynamic Programming)과 헷갈려 하는 분들이 좀 있는데 문제를 서브로 나누는건 맞는데 둘의 가장 큰 차이점은 하위문제(sub problem)의 해가 다른 하위문제에 디펜던시가 있으면 안된다는 것이다.
즉, 분할정복 알고리즘은 문제해결을 위해 하위문제를 분할하고 하위문제의 해가 다른 하위문제를 풀기 위해 사용되지 않고 독립적으로 가능한 것을 말하고 동적프로그래밍은 하위문제의 해가 다른 하위 문제를 푸는데 필요한 경우를 말한다.
분할정복은 보통 3가지 단게를 거친다.
ⓑ 정복(conquer) 단계 : 각각의 작은 문제를 동일한 방법으로 순환적(recursive)으로 해결
ⓒ 합졍(merge) 단계 : 작은 문제의 해를 합하여(merge) 원래 문제에 대한 해를 구함
앞으로 분할정복 (Divide & Conquer) 카테고리에 다양한 알고리즘 문제를 다루어 보면서 정복해 나가도록 하자.