Q. 그래프에서 사이클이 이란 ?
그래프의 특정 정점에서 출발하여 돌아다니다가 다시 처음 출발했던 곳으로 되돌아 갈 수 있으면 사이클이 있다고 한다.
그림1에서 (a)는 Tj(출발) → Tn → Tm → Tj(출발지점으로 다시 돌아옴) 으로 순환되는 사이클이 있지만 (b)는 어디에서 출발하던 출발지점으로 다시 돌아올수 있는 방법이 없다. 즉 사이클이 존재하지 않는다.

[출처] https://www.researchgate.net/figure/Example-of-cyclic-and-acyclic-graphs_fig2_2431833
Q. 사이클을 찾는다는 것은?
사이클을 검출(detect) 한다는 것은 그래프내에 사이클이 있는가? 있다면 총 몇 개 존재하는가 ? 그리고 사이클에 포함된 노드의 개수는 몇 개인가? 등을 알아내는 것이다.
어떠한 이유로 그래프 자료구조를 이용해 다양한 문제를 풀다보면 그래프내 사이클을 찾는 알고리즘들이 필요하게 된다.
예를들어 최소신장트리 - MST를 생성하려면 그래프내 사이클이 없어야 하는데 MST를 생성하는 알고리즘 중 하나인 크러스컬(Kruskal) 알고리즘 에서도 필요하다.
사이클을 검출하는 방법이 몇가지 있는데 여기서는 다양한 에제를 통해 사이클 검출하는 알고리즘을 확인해 보자.
Q. 서로수집합(Disjoint Set) - 합집합-찾기(union–find) 으로 사이클 검출이 가능하다고 하던데 ?
Disjoin Set에 대해서 모르면 우선 서로수집합(Disjoint Set) - 합집합-찾기(union–find)를 반드시 선행 학습해야 한다.
서로수 집합의 원소를 정점(or 노드)라고 하면 같은 집합(subgraph)에 포함되어 있는 정점들끼리는 이미 에지로 연결된 것들이고 다른 집합(subgraph)에 있는 정점과는 서로 연결되어 있지 않다는 것을 기반으로 한다.
Union-Find Algorithm 은 그래프내 셀프루프(self-loop : 자기자신을 가리키는 간선)을 포함하면 안되고 무방향그래프에서 사이클을 찾는데 유용하다.
그림 2와 같은 그래프가 있을때 0 → 1 → 3 → 2 → 0 으로 순환되는 사이클이 1개 존재하는데 이것을 Union-Find Algorithm으로 검출하는 것을 예로 들어보자.
처음에는 정점들을 disjoint set 들로 만들기위해 루트노드가 자기자신을 가리키는 트리 5개가 만들어진다.

그림2는 S1 ∪NION S0 = {0, 1} 을 하고 0을 부모로 한다.

disjoint set 에서 UNION을 하려면 서로 연결하려는 정점의 루트노드가 서로 달라야 한다
여기서 S1, S0 는 서로 루트노드가 다르기 때문에 UNION이 가능하다. (서로수집합(Disjoint Set) - 합집합-찾기(union–find) 코드 참고)
|
1
2
3
4
5
6
7
8
9
|
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
count--;
}
|
그림3는 S2 ∪NION S0 = {0, 1, 2} 을 하고 0을 부모로 한다.

그림4는 S3 ∪NION S0 = {0, 1, 2, 3 } 을 하고 1을 부모로 한다.

그림5는 S4 ∪NION S0 = {0, 1, 2, 3 } 을 하고 3을 부모로 하였다.
이제 모든 정점에 에지가 연결되었고 사이클이 없는 스패닝트리(spanning tree)가 완성되었다.
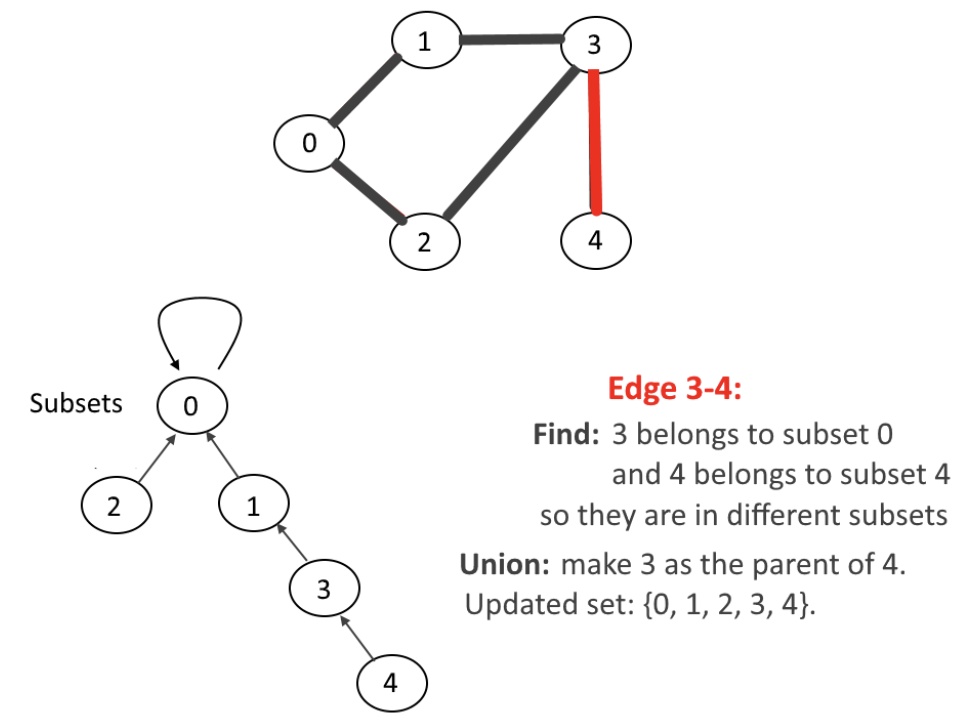
그림6은 3 -> 2를 에지를 연결하려 시도하고 있다.
Union-Find Algorithm 을 이용하여 3과, 2의 루트노드를 찾아볼것이다.
3, 2는 루트노드 0의 자식노드 또는 손자노드이기 때문에 같은 집합에 있다.
disjoint set 에서 UNION을 하려면 서로 연결하려는 정점의 루트노드가 서로 달라야 한다는 규칙을 어기게된고
이런경우 사이클이 생성된것을 알아낼 수 있다.

Q. DFS깊이우선탐색(DFS, Depth First Search) 로 사이클 검출이 가능하다고 하던데 ?
DFS를 모르면 우선 DFS깊이우선탐색(DFS, Depth First Search)를 선행 학습해야한다.
dfs는 그래프의 모든 정점을 에지의 방향에 따라 순회하면서 백에지(bak dege)가 있으면 사이클이 있다고 판단한다.
.....
레퍼런스
- Graph – Find Cycle in Undirected Graph using Disjoint Set (Union-Find)
- Graph – Detect Cycle in Undirected Graph using DFS
- Tree, Back, Edge and Cross Edges in DFS of Graph
- https://www.geeksforgeeks.org/detect-cycle-in-a-graph/
'알고리즘(Algorithm) > 그래프(Graph)' 카테고리의 다른 글
| [그래프]길찾기 bfs 알고리즘(maze algorithm) (3) | 2019.08.01 |
|---|---|
| [그래프] 위상 정렬(Topological Sort) - Kahn's algorithm (0) | 2019.07.04 |
| [그래프] 모든 정점의 indegree 계산 (0) | 2019.07.04 |
| 그래프(Graph)-너비우선탐색(BFS, Breadth First Search) algorithm (0) | 2019.07.02 |
| 그래프(Graph)-깊이우선탐색(DFS, Depth First Search) (0) | 2019.07.02 |


