자료구조 그래프에서 모든 정점을 순회하기 위한 방법으로 너비우선탐색(BFS, Breadth First Search) algorithm
과 깊이우선탐색(DFS, Depth First Search) 알고리즘을 알아 봤었다.
이 bfs 와 dfs 알고리즘은 길찾기 (미로 탈출) 에도 유용하게 사용되는데 이 post 는 bfs 를 통해 길찾는것을 설명하겠다.
우선 그림 1과 같은 미로가 있다고 가정하자. 설명을 빨리 하기위해 매우 단순한(?) 미로를 선택하였다.

미로를 자료로 표현하기 위해 graph 로 표현할수 있지만 행렬(matrix)로 도 가능하다. 여기서는 행렬로 하겠다.
7X7 미로인 위 그림을 행렬로 표현하면 다음과 같다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0(★입구) | 1 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 | 0 | 0(●출구) | 1 |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1은 갈수 없는 길 즉 벽(wall) 이고, 0을 갈수 있는 길 (path)이라고 생각하면 된다.
그럼 그림1 에서 처음 길을 찾기위한 엔트리 포인트(별모양)는 (5, 1) 좌표에 있고 우리가 갈 목적지 = 출구 = EXIT (동그라미)는 (5,5) 좌표에 있는것을 알수 있다.
이제부터 bfs 를 통해 길을 찾아보는 알고리즘을 살펴보자
좌표(x,y)로 하려고 하다가 행렬 위치를 찾는데 눈이 아파서 그림 2처럼 알파벳으로 표현했다.
입구는 A 니 A 를 큐에 넣는다. 큐에 넣고 해당 위치는 이미 방문한 적이 있는 놈이라고 표시를 해준다(그림에서는 노란색바탕으로 표현)
그리고 어찌 보면 당연한건데 이미 해당 지점에서 어떤 길로 갈지 결정을 한 상태이기 때문에 다시 돌아와서 어떤길로 갈지 다시 선택할 필요가 없단 말이다.
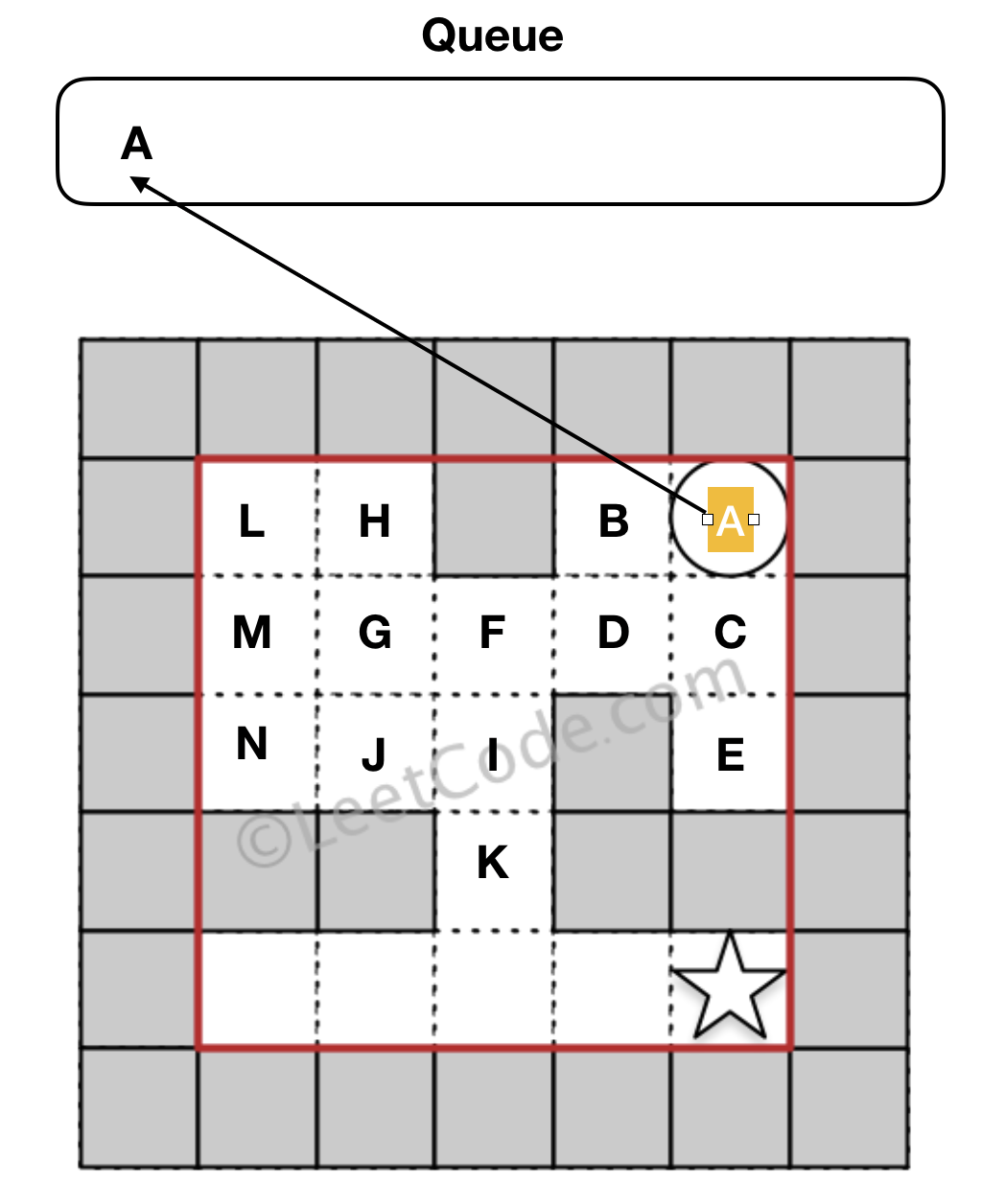
A 와 인접한 사각형중 벽이 아닌 놈은 B, C 다.
그럼 우린 A -> B 로 길을 찾는 경우와 A -> C로 길을 찾는 경우를 모두 탐색해볼 수 있게 된다.
그리고 A와 인접한 것을 A -> B 처럼 연결리스트로 계속 이어 붙이면 나중에 목적지에 도착했을때 내가 어디 어디를 거쳐서 목적지 까지 오게 되었는지 알수 있게 된다.
암튼 큐에서 A빼고 A와 인접한 칸 B, C를 큐에다 다시 넣는다. (왜 이렇게 해야하는지 이해가 안가면 너비우선탐색(BFS, Breadth First Search) algorithm 을 반드시 읽어야 한다.)
그리고 방문한 칸이라고 표시해주자. 그림 3은 현재 상태를 보여준다.

그럼 A -> B -> D 까지 온 것이다.

그럼 A -> C - > E 까지의 경로가 또 하나 생겼다.

A -> B -> D -> F 까지 왔다. ^^
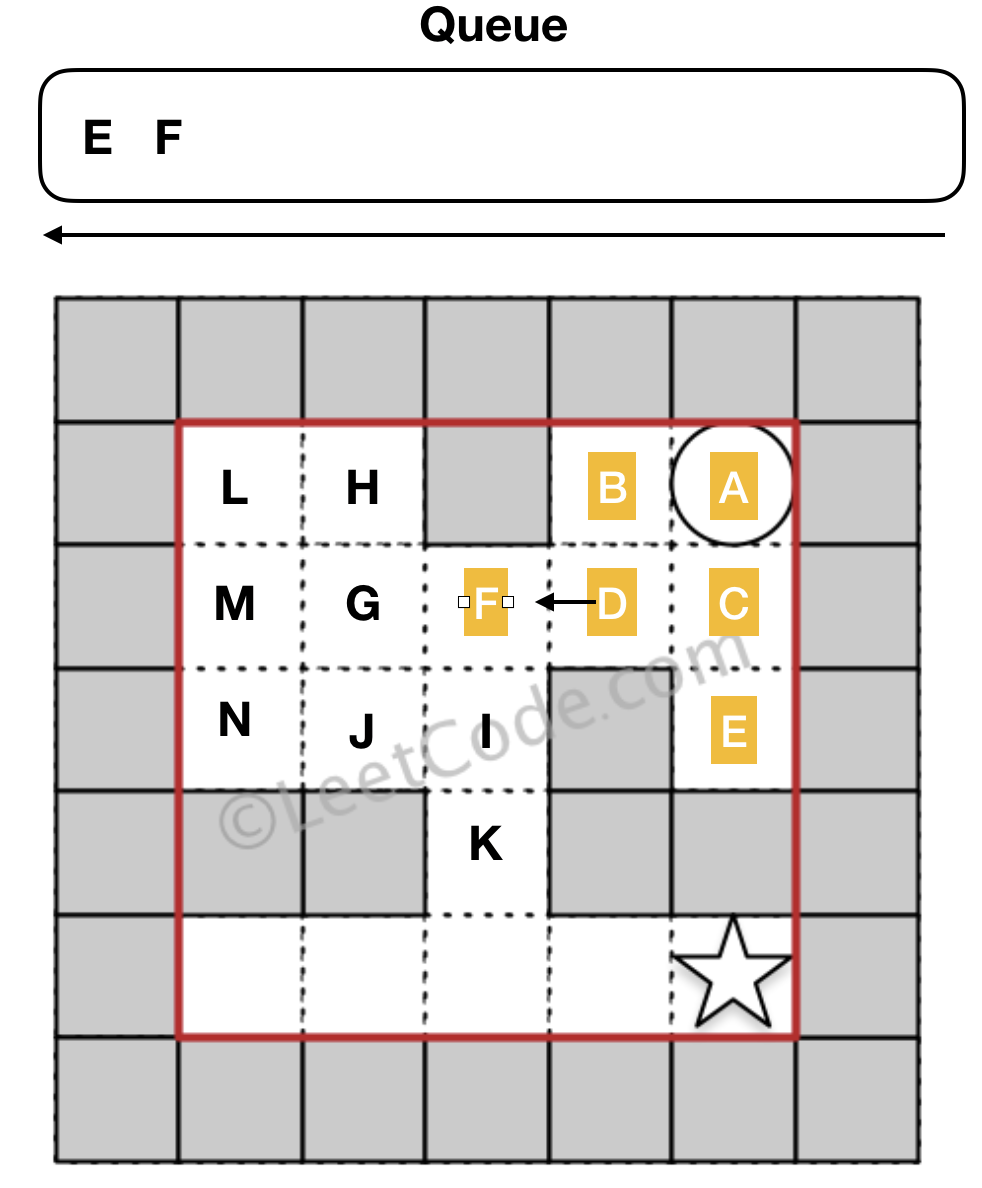

그림8. 큐에서 F를 빼고 인접한 칸중 벽이 아닌 G, I 를 큐에 넣고 방문표시해준다.
참고로 인접한 칸중 어느것부터 넣을지 궁금할텐데 답은 없다. 그냥 인접한 칸중 방문한 적이 없는 칸을 빼놓지 않고 큐에 넣어줘야 한다는 것만 지키면 된다. 예를들어 동,남,서,북으로 검사하여 벽이 아니면 큐에 넣어도 되고 동서남북으로 해도 된다.

글이 길어져서 더이상 그림과 설명은 생략한다. 머릿속으로 상상해보면 된다.
그럼 위 알고리즘을 코드로 구현하자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
|
public class MazeMain {
public static void main(String[] args) {
// 7x7 미로
int [][] maze = {
{1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1}
};
List<Node> paths = bfs(maze);
System.out.println(paths); // 입구->출구까지 이동한 위치 정보
// 출력 - output
// 이동거리 9
// [(5, 1), (5, 2), (4, 2), (3, 2), (3, 3), (3, 4), (3, 5), (4, 5), (5, 5)]
}
/**
* maze[][] 에서 1칸(x,y) 를 나타내는 Node 클래스
* */
public static class Node {
int x; // 칸의 x 좌표
int y; // 칸의 y 좌표
// 이동한 경로를 연결리스트로 나타내기 위해 이전 Node를 참조하기위한 변수
Node prev;
Node(int x, int y, Node prev ) {
this.x = x;
this.y = y;
this.prev = prev;
}
@Override
public String toString() {
return String.format("(%d, %d)", x, y);
}
}
public static List<Node> bfs(int[][] maze) {
// 방문한 노드인지 체크하기 위한 변수.
int row = maze.length;
int col = maze[0].length;
// 방문한 노드는 true 로 표시하기위한 변수
boolean[][] visited = new boolean[row][col];
// (x1,x2) -> (N,N)로 가기 위한 경로를 연결리스트로 저장
List<Node> paths = new LinkedList<>();
// bfs 를 위해 큐가 필요하다.
Queue<Node> queue = new LinkedList<>();
// 출발지는 (5,1) 부터이다.
visited[1][5] = true;
// 현재 방문중인 노드의 인접노드들중 벽(Wall)이 아닌 길(Path)가 어디있는지 확인하기위해
// 현태 (x,y) 에서 서->남->동->북 으로 탐색하기위한 거리 배열 변수.
int dist_x[] = { 1, 0, -1, 0};
int dist_y[] = { 0, 1, 0, -1};
while(!queue.isEmpty()) {
// 현재 큐에 있는 것을 꺼낸다.
Node node = queue.poll();
// 만약 node가 -> 출구까지 왔는지 체크한다..
if(node.x == 5 && node.y == 5) {
// 출구까지 왔으면 출구까지 오기전에 이전칸은 무엇이고 그 이전칸은 무엇인지
// 거꾸로 prev 노드를 올라가면서 list 에 추가하고 탐색을 마무리 한다.
Node s = node;
while(s != null) {
paths.add(0, s);
s = s.prev;
}
break;
}
// 출구까지 온게 아니면 현재 칸(노드)에서 인접한 노드를
// 서 -> 남 -> 동 -> 북 순으로 검사해본다.
for(int i = 0 ; i < dist_x.length ; i++) {
int vx = node.x + dist_x[i];
int vy = node.y + dist_y[i];
// 인접한 (vx, vy) 노드기 이전에 방문하였거나 wall 이면
if(is_path(vx , vy, maze, visited, row, col)) {
visited[vy][vx] = true;
queue.offer(new Node(vx, vy , node));
}
}
}
return paths;
}
/**
* @return maze 영역을 벗어나거나 이미 방문한 노드가 아니면 true
*/
public static boolean is_path(int x, int y,
int[][] board,
boolean[][] visited,
int row, int col) {
// maze 영역을 벗어나면 안됨.
if(x < 0|| y < 0 || x > col -1 || y > row - 1) {
return false;
}
// 이미 방문한 노드도 안됨. wall 은 갈수 없음.
if(visited[y][x] || board[y][x] == 1) {
// [row][column]
return false;
}
return true;
}
}
Colored by Color Scripter
|
'알고리즘(Algorithm) > 그래프(Graph)' 카테고리의 다른 글
| [그래프] 그래프에서 사이클 찾는 방법들(Detect Cycle in an Graph) (0) | 2019.07.06 |
|---|---|
| [그래프] 위상 정렬(Topological Sort) - Kahn's algorithm (0) | 2019.07.04 |
| [그래프] 모든 정점의 indegree 계산 (0) | 2019.07.04 |
| 그래프(Graph)-너비우선탐색(BFS, Breadth First Search) algorithm (0) | 2019.07.02 |
| 그래프(Graph)-깊이우선탐색(DFS, Depth First Search) (0) | 2019.07.02 |


