순열(Permutation)

목차

1. 경우의 수 - 합의 법칙경우의 수 - 합의 법칙 
2. 순열(Permutation) <- 여기
3. 순열 - 이웃조건 
4. 원순열
5. 원순열 - 다각형 순열
6. 같은 것이 있는 순열 
7. 중복순열 

수학에서, 순열(permutation)이란 어떤 임의의 것들에 순서를 부여하여 나열하는 것이라고 생각하면 된다.

Q. 예를들어 A, B, C, D 4명이 있는데 이들을 일렬로 나열하기 위한 경우의 수를 구하는 것을 생각해보자  

 

우선 4명을 일렬로 나열해야하니 빈칸 4개를 그려보자

 

• 맨 앞에는 4명중 1명이 올수 있고 B를 선택  (여기서 일어날 수 있는 경우의 수는 4)
• 그 다음에는 B 를 제외한 3명중 한명이 올 수 있고 D를 선택  (여기서 일어날 수 있는 경우의 수는 3)
• 그 다음에는 B, D 를 제외한 2명 중 한명이 올 수 있고 A를 선택 (여기서 일어날 수 있는 경우의 수는 2)
• 그 다음에는 B, D, A를 제외한 3명중 한명이 올 수 있고 C를 선택한다고 가정하자  (여기서 일어날 수 있는 경우의 수는 1)

각 경우의 수를 포함하는 사건이 동시에 즉,  연달아 일어나야 하기 때문에 일렬로 나열할 수 있는 총 경우의 수는 

 

4 x 3 x 2 x 1 = 4! (4팩토리얼) = 24가지가 된다.

따라서 임의의 것들에 대한 순서를 부여할 때 나올수 있는 총 경우의 수 공식은 

 

n! = n x (n-1) x .... 2 x 1 로 나타낼수 있다.

 

문제 확장을 좀 더 해보자 

 

Q. A, B, C, D, E 5명이 있는데 이 중 3명만 뽑아서 일렬로 세울 수 있는 경우의 수는 총 몇가지인가 ?

 

• 첫번째는 5명중 한명이 올 수 있고 ( 경우의 수 = 5)
• 두번째는 4명중 한명이 올 수 있고 (경우의 수 = 4 )
• 세번째는 3명중 한명이 올 수 있다 (경우의 수 = 3)

 

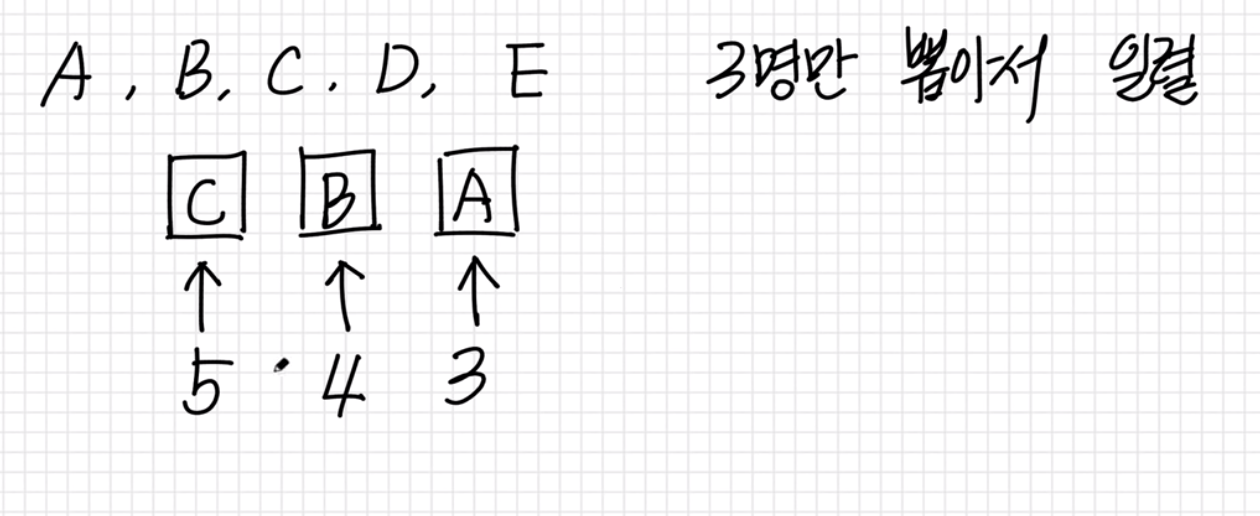
따라서 각 경우의 수를 포함하는 사건이 동시에 일어나는 것을 구하면 5 x 4 x 3 = 60 가지가 되고  팩토리얼로는 5!/2!로 나타낼수있다.

그리고 이 처럼 5가지중에 3개를 뽑아 만들수 있는 경우의 수를 수학에는  ₅P₃로 표현하고 공식식은 아래와 같다.

n개 중에서 r 개를 뽑아서 일렬로 나열하는 경우의 수를  nPr 로 표기하고 계산은 n!/(n-r)!  와 같다.

nPr = n!/(n-r)! 

 

레퍼런스

• 수학중독- 순열(Permutation)