Q. 백트래킹이란 ?
지금은 네비게이션이 잘 발달 되어 있으니 설명이 애매하지만 네비게이션도 없고 지도도 없는 세상에 왔다.
A출발점에서 B 목적지까지 아무것도 없이 걸어서 또는 자전거를 타고 여행을 간다고 생각하면 일단 직관적으로 아 이쪽길로 가면 목적지에 가겠지 하고 가본다.
그런데 도착해서 동네사람들에게 물어보니 이동네는 그 동네가 아니라고 하면 선택은 다른 갈림길로 가던지 일단 왔던길을 되돌아가서 이쪽길은 절대가면 안되는길이라고 뭔가 표식을 달아 놓고 다른 길로 가는 선택을 할 수 있겠다.
물론 길을 선택하는데 앞에 강이 있거나 큰 바다가 있거나 높은 산이 있거나(제약조건) 등... 어떠한 이유로 갈수없는것들은 목숨걸고 갈필요 없이 포기하고 빨리 다른길을 선택 할 수도있다.
이리저리 이길 저길 다 돌아다니다보니 최종 목적지 B 에 오게 되다.
위 내용이 사실 백트래킹 알고리즘의 전부인데 컴퓨터 분야에서 백트래킹은 아래처럼 정의하고 있다.
Backtracking can be defined as a general algorithmic technique that considers searching every possible combination in order to solve a computational problem.
해석하면 백트래킹은 일반적인 알고리즘 기법이다.
어떤 기법이냐 하면 문제를 푸는데 있어 고려할 수 있는 모든 경우의 수를 모두 검색해보는 기법이란 말이다.
이렇게 하다보면 언젠가 답은 나오겠지 하는 기법이단 말이다.
그래서 보통 백트레킹은 Decision Problem, Optimization Problem, Enumeration Problem 등에 주로 사용된다.
모든 문제에 한가지 솔류션만 있는것이 아니니 이런 문제는 무조건 백트래킹으로 풀어라 라고 할수는 없고 constraint satisfaction problem(CSP) 들을 백트래킹 알고리즘으로 접근하면 좋다.
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations.
즉, 정리하면 백트래킹이란? 문제를 풀면서 이조건 저조건 고려하다보니 다양한 상태(경우의 수)가 생기는데 그 상태가 내가 찾는 답인지는 특정 제약(constraints) 또는 제한(limitations)을 반드시 만족해야만한다.
그래서 조건을 만족할만 한 후보로 점진적으로 나아가다가 어느 순간 유효한 것으로 완료 될 수 없다고 판단되는 즉시 ("백 트랙" <- 다시는 이길로 오지마 하고 표기하는거)이를 포기하고 다른 후보로 점진적으로 나아가면서 결국 최적의 해를 찾는 것이다.
Q. 그럼 백트래킹을 위해 모든 경우의 수를 만들어야 하는데 어떻게 만들면 되지?
문제마다 경우의 수나 제약이 다 다르니 이건 케바케이다.
뭔가 답이 정해져 있지 않다는 얘기이다. 약간 머리를 굴려야 하는 일도 있을것이고..
다만 문제를 풀기위해 어떤 자료구조로 경우의 수를 만들면 좋을까? 가 더 알맞은 질문인거 같다.
보통 백트래킹을 위해 고려해야할 모든 경우의 수를 상태공간트리(State Space Tree)라는 걸로 표현한다.
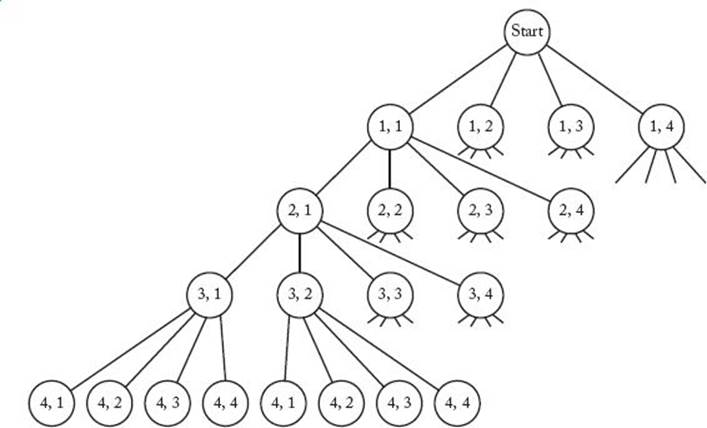
그림1 은 백트래킹 문제중 대표적 n -Queens 문제를 (사실 재귀로도 풀수있다) 위한 모든 가능한 경우의 수를 상태공간트리로 표현한것이다. n -Queens 문제가 뭐고 그림이 정확히 어떤 경우의수(상태들)를 트리로 구성한건지 이해할 필요는 없다.
단 백트래킹을 문제를 접근하기위해 상태공간트리를 이용한다는것과 트리 자료구조를 이용한다는 것만 알고 있으면된다.
Q. 상태공간트리를 만들었으면 그 길이 올바른 길인지 아닌지 어떻게 탐색하나?
트리는 모든 정점을 포함하고 & 정점간 서로 연결(connected)되어 있고 & 사이클(cycle)이 없는 그래프이다.
따라서 상태공간트리에서 각 상태(정점)들을 하나하나 방문하면서 제약(constraints) 또는 제한(limitations)을 만족하여 앞으로 답이 될수 있는 후보인지 아닌지 점짐적으로 탐색해 나가면 된다.
여기에 힌트가 있는데 그래프를 탐색하기위한 방법은 깊이우선탐색(Depth First Search, DFS)과 너비우선탐색(Breadth First Search, BFS), 최선 우선 탐색(Best First Search/Heuristic Search)이 있는데 문제에 따라 적절히 선택하면 된다.
이건 백트래킹 문제를 살펴보면서 어떤 탐색이 유리한지 알게 될 것이다.
Q. 그럼 백트래킹이 그래프를 dfs 나 bfs 로 탐색하는것과 뭐가 다른가?
사실 거의 비슷한데 그래프에서 DFS, BFS 는 모든 정점을 탐색하는 과정이라면 백트래킹은 모든 정점을 탐색하지 않고 상태공간트리를 탐색하다가 제약이 맞지 않으면 해의 후보가 될만한 곳으로 되돌아가서 다시 탐색하는 방법이다.
탐색하는데 dfs, bsf를 사용하는 것 뿐이지 탐색하다가 이길은 아닌가벼 생각들면 과감히 포기하고 다른길로 되돌아가는게 다른점이다.
이 길이 정답이 있을 만한 후보가 안되면 과감히 포기하고 빨리 다른길로 돌아서 탐색의 시간을 절약하기위한 것을 백트래킹에서 가지치기(pruning) 라고 부르고 후보가 될만한 놈인지 아닌지 검사하는 것을 Promising 이라고 한다.
Q. 백트래킹 알고리즘의 의사코드는 ?
문제마다 변형이 필요해 100%는 아니지만 대부분 아래와 같은 의사코드로 백트래킹을 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
BACKTRACKING(G):
if(..) {
If at a solution, return scueess
}
for (every possible chioce from current state / node) {
if(Promising)) {
BACKTRACKING(G)
}
else {
Back out of the current choice to resotre the state at the begining of the loop
pruning
}
}
BACKTRACKING()
Colored by Color Scripter
|
마지막으로 그림2는 sudoku를 백트래킹을 통해 상태를 검사하면서 푸는 애니매이션이다.

[출처] : https://en.wikipedia.org/wiki/Backtracking