N-Queen 문제는 재귀문제중 매우 대중적인 문제인데 어떤 문제인지 파악부터 해보자.
N-Queen 문제는 N x N 크기의 체스판에 N 개의 퀸을, 서로 공격할 수 없도록 올려놓는 솔류션을 구하는 문제이다.
예를들어 8x8 체스판이 있다면 그림1. 처럼 Queen은 N=8개가 놓일 수 있는데 이게 맘대로 배치하면 안되고 특정 규칙에 따라 배치해야 한다.

특정 규칙이라는것은 그림2처럼 Queen 이 배치 될때 같은 행(row), 열(column)에 다른 Queen이 있으면 안되고 대각선(diagonal) 으로도 있으면 안된다는 것이다.

[출처] https://helloacm.com/n-queen-problem-in-back-tracing-bit-logics/
여기까지 왔으면 문제는 다 파악된것이다.
요약하면 NxN 체스판에 N개의 Queen을 배치해야 한다. 단, N개의 Queen은 행, 열, 대각선으로 서로 겹치면 안된다는것이다.
그림3을 규칙에 어긋나지 않도록 8x8 체스판에 Queen=8 개를 배치한 결과인데 당연히 솔류션은 1개만 있는것이 아니다. (여기서는 12가지가 있다)

[출처] http://mathworld.wolfram.com/QueensProblem.html
이 문제는 재귀적인 패턴을 가지고 있는가 ? 가지고 있다면 재귀를 탈출하는 base case는 무엇인가? 생각해보자.

체스판에 Queen 이 놓을수있는 모든 경우의수를 생각하면 첫번째에 1~8 칸에 Queen을 놓을수 있고 두번째칸에도 1~8칸에 놓을수 있고 .... Nth 까지 이어진다. 그림4는 이런 과정을 상태공간트리(State Space Tree)로 나타낸 것인데 체스판에 Queen 이 놓을수있는 모든 경우의수를 고려한 트리라고 생각하면 된다.
상태공간트리를 재귀적으로 하나 하나 확인해보다가 N=8개가 다 배치되었다면 재귀는 끝난다.
따라서 base case 는 Queen 이 N개만큼 배치되었냐를 확인하면된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
public class NQueenMain {
public static void main(String[] args) {
int N = 6;
// cols 는 체스판에 Queen 이 각 row 마다 어디에 놓여있는지를 저장하는 변수임.
// 즉, cols[1] = 2 이면 (1,2)에 있다는 의미이다.
int cols[] = new int[N];
queens(0, N, cols);
}
/**
* @row chess판에 현재 Queen이 놓일 행(row) 위치
* @N chsess 판의 크기 or chess 판에 놓여질 Queen의 총 개수.
* @cols 현재까지 체스판에 Queen 이 놓여진 데이터 즉, cols[1] = 2 이면 (1,2)에 있다는 의미이다.
* */
public static void queens(int row, int N, int[] cols) {
if(row >= N) {
for (int i = 0; i < N; i++) {
// chess판에 놓여진 N개의 Queen 위치를 출력한다.
System.out.println(String.format("(% d, %d)", i+1, cols[i]+1));
}
System.out.println("###################");
return;
}
// 상태공간 트리에 따라 하나씩 재귀적으로 탐색하는 코드.
for(int col = 0 ; col < N ; col++) {
// row-ith 놓일수 있는경우의 수 1부터 8까지를 모두 검토해본다.
// 대신 해당 자리가 문제가 없는지 검사를 먼저 하고 문제가 없는경우만 다음 row 를 검사하도록한다.
cols[row] = col;
if(promising(cols, row , col)) {
queens(row + 1, N, cols);
}
}
}
/**
* row, col 에 놓일 Queen의 위치가 이전에 놓인 Queen들과
* 행,렬, 대각선으로 겹치지 않는지 판단한다.
* 만약 겹친다면 false를 겹치치 않는다면 true 를 리턴한다.
* */
public static boolean promising(int[] cols, int row, int col) {
for (int i = 0 ; i < row ; i++) {
if (cols[i] == col) // 같은 열에 놓였는지 검사
return false;
return false;
}
}
return true;
}
}
Colored by Color Scripter
|
위 코드는 Queen이 놓여질 솔류션들을 모두 출력해주는 코드이다.
체스판 크기에 따른 솔류션 개수는 다음과 같다.

코드중 promising() 메소드가 이해가 잘 안갈 수 있는데 우선 if (cols[i] == col) 부분은
같은 column 에 놓여있는 Queen 이 있는지 체크하는 것이고 if ((row - i) == Math.abs(col - cols[i]) 에서
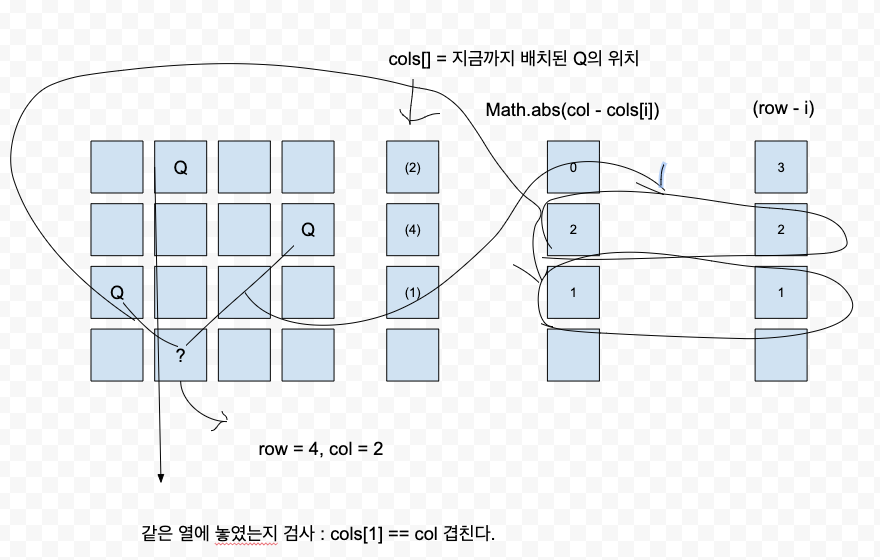
NxN 정사각형이기 Queen이 (row, column)에 배치되었을 때 해당 위치에서 대각선을 연장해서 쭉그려보면 함수의 기울기가 1이기 때문에 겹치는 영역은 Math.abs(col - cols[i])/(row - i) = 1 이 있을것이다.
따라서 Math.abs(col - cols[i]) == (row - i) 가 같은지 확인하는 것이다.
만약 NxN 처럼 정사각형이 아니라면 이 코드는 수정되어야 한다.
'알고리즘(Algorithm) > 재귀(recursion)' 카테고리의 다른 글
| (재귀)피보나치 수열(Fibonacci Sequence) (0) | 2019.06.25 |
|---|---|
| (재귀)Blob(Labeling) 알고리즘 (0) | 2019.06.25 |
| (재귀)미로(MAZE)찾기 (0) | 2019.06.25 |
| 재귀함수(Recursive Function)란? (0) | 2019.06.25 |


