동적 프로그래밍 basic 문제-이항계수(Binomial Coefficient) - DP1

동적프로그래밍(Dynamic Programming)이란? 에서 동적프로그래밍이 무엇인지 알아보았고 동적 프로그래밍 문제를 해결하는 방법 에서는 dp 문제를 어떻게 접근해서 풀어야 하는지 설명하였다.

 

여기서는 기본적인 dp 문제를 풀어보면서 감을 익혀보자.

이항계수((Binomial Coefficient)

조합론에서, 이항 계수(二項係數, 영어: binomial coefficient)는 주어진 크기의 (순서 없는) 조합의 가짓수라고 정의되어 있다.
즉, 전체 집합에서 원소의 개수 n에 대해 r개의 아이템을 뽑는 이항계수(조합의 수)는 수학에서 다음과 같이 정의된다.
공식에 대한 자세한 설명은 생략한다. 

이것을 재귀로 풀면 다음과 같다.

int binomial(int n, int k) {
 if (n == k || k == 0)
     return 1;
 else
     return binomial(n - 1, k) + binomial(n - 1, k - 1);
}

그림1

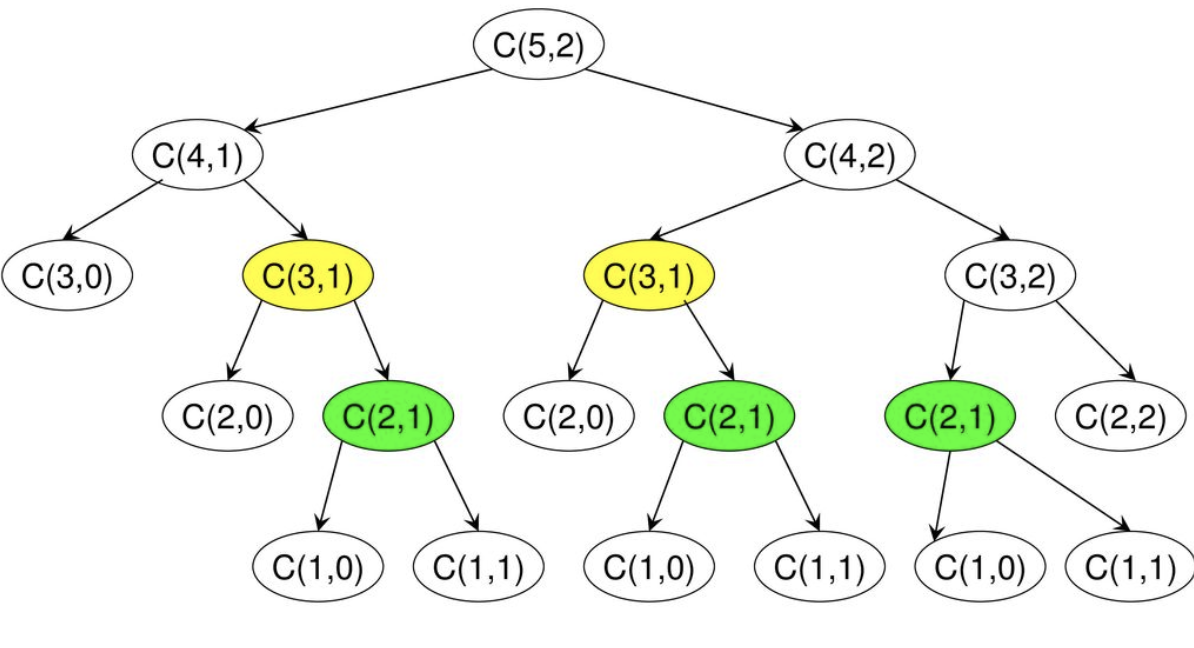
효율을 높이기위해 이항계수는 하위문제를 이용해서 최종결과의 해를 구할수 있는 dp 문제로 접근하여 풀면 된다. 
이전계산 결과값을 메모이제이션(탑다운)을 이용하여 풀경우 코드는 

int binomial(int n, int k) {
 if (n == k || k == 0)
     return 1;
 else if (binom[n][k] > -1) /* 배열 binom이 -1로 초기화되어 있다고 가정 */
     return binom[n][k];
 else {
     binom[n][k] = binomial(n-1, k) + binomial(n-1, k-1);
     return binom[n][k];
 }
}

 바텀업(bottom up)방식으로 풀경우는 다음과 같다. 

int binomial(int n, int k) {
 for (int i=0; i<=n; i++) {
     for (int j=0; j<=k && j<=i; j++) {
         if (k==0 || n==k)
             binom[i][j] = 1;
         else
             binom[i][j] = binom[i-1][j-1] + binom[i-1][j];
     }
 }
 return binom[n][k];
}

bottom up 으로 할때 현재 상태의 문제를 풀때 항상 이전 값이 있어야만 되는데 그림 2처럼  binomial(5,3) 의 해를 구하기위해 
binomial(4,2), binomial(4, 3) 이 필요하고  binomial(4,2) 는 binomial(3,1) 과 binomial(3, 2) 이 필요하다.
이렇게 계속 올가가다 보면 (0,0) -> (1,0) (1,1)  -> (2,0), (2,1), (2,2) 순으로 차례차례 구해놓으면 된다. 

그림2

 

 

레퍼런스

• 알고리즘 강좌 - 동적계획법(Dynamic Programming)
• Binomial Coefficient | DP-9