호너의 법칙(Horner's method)

호너의 법칙은 영어로  Horner's rule (or Horner's method, Horner's scheme)라고 불리는데 다항식을 푸는데 계산량을 줄일수 있는 방법이다.

 

일반적으로 그림1과 같은 다항식이 있다고 가정하면 차수가 가장 높은것부터 낮은것까지 하나씩 계산하면서 모두 더해주면 된다. 

그림1

 

[출처] Horner`s Rule for Polynomial Computation

 

예를들어 5x⁴ + 2x³ – 3x² + x – 7 가 있고 x = 3이라고 하면 그림2처럼 계산되고 결과 값은 428이 된다.

그림2

 

이 방법으로 프로그래밍하면 다음과 같고 

 
public class Polynomial {
 
 
    /**
     * @param  coefficients 는 다항식 각 차수의 계수이다.
     * @param x
     * */
    public static void computePolynomial(double[] coefficients, double x) {
 
        int totalAdditions = 0;
        int totalMultiplications = 0;
 
 
        int n = coefficients.length - 1;
        double result = 0.0;
        for(int i = n; i >= 0; i-- ) {
            result += coefficients[i]* Math.pow(x, i);
            totalAdditions += 1;
            totalMultiplications += i ;
        }
 
        System.out.println(String.format("result=%.2f, " +
                "total addition = %d, " +
                "total multiplication = %d", result, totalAdditions, totalMultiplications));
    }
 
 
    public static void main(String[] args) {
        double[] examplePoly = new double[]{ -7, 1, -3, 2, 5 };
        Polynomial.computePolynomial(examplePoly, 3);
    }
 
}

출력은 result=428.00, total addition = 5, total multiplication = 10 나온다. 일반적으로 하면 더하기 5번, 곱하기 10번이 필요하다. 

따라서 이방식으로 했을때 n차수(n-degree)의 다항식에서 필요한 덧셈과 곱셈의 횟수는 그림 3처럼 된다. 

그림3

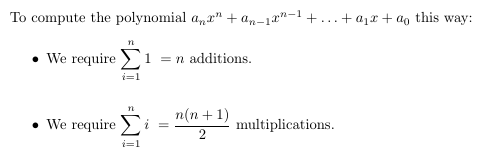
답은 정확한데  작은 다항식에도 대해 꽤 많은 곱셈이 필요한 것을 알 수 있다.

곱셈을 줄이기위한 방법을 고민해야하는데 가장 먼저 생각할수 있는것은 이전에 계산된 연산을 저장해놨다가 다음 계산에 사용하는것이다.

그림 4는 다항식에서 미리 계산된값을 캐싱해놨다가 다음 계산에서 사용하고 있는것을 보여준다.

 

그림4

이것을 사용하여 위의 다항식 계산에 적용한다면 그림5와 같은 계산과정을 거치게 된다.

 

이 방법으로 구현해보자 

 

 
public class Polynomial {
 
 
    /**
     * @param  coefficients 는 다항식 각 차수의 계수이다.
     * @param x
     * */
    public static void computePolynomial(double[] coefficients, double x) {
 
        int totalAdditions = 0;
        int totalMultiplications = 0;
 
 
        int n = coefficients.length - 1;
 
        double result = coefficients[0];
 
        double powerOfX = 1.0;
        for (int i = 1; i <= n; i++) {
            powerOfX *= x; // caching
            result += coefficients[i] * powerOfX;
            totalAdditions += 1;
            totalMultiplications += 2;
        }
 
 
        System.out.println(String.format("result=%.2f, " +
                "total addition = %d, " +
                "total multiplication = %d", result, totalAdditions, totalMultiplications));
    }
 
 
    public static void main(String[] args) {
        double[] examplePoly = new double[]{ -7, 1, -3, 2, 5 };
        Polynomial.computePolynomial(examplePoly, 3);
    }
 
}
 

powerOfX 변수를 사용하여 이전 x 항을 계속 유지하므로 다항식의 다음 항을 계산할 때 재사용할 수 있게 되었다.

이것은 결국 우리가 하는 곱셈의 수를 줄이는데 도움을 준다. 

출력은 result=428.00, total addition = 4, total multiplication = 8 이고 이전보다 더하기, 곱셈의 수가 줄어든것을 알수 있다.

곱셈값을 미리계산하는 방식으로 했을때 n차수(n-degree)의 다항식에서 필요한 덧셈과 곱셈의 횟수는 그림 4처럼 된다. 

그림4

 

호너의 법칙(Horner's method)을 이용하면 곱셈의 수를 더 줄일수 있게된다. 

호너의 법칙은 그림 5의 아래등식처럼 기존의 다항식과 동일하게 재 작성할수 있게 되고 재작성된 식으로 다항식을 계산한다면 n차수 다항식에서 n 곱셈과  n 덧셈만으로 차수 n의 다항식을 평가할 수 있게 된다.

그림5

 

 

계산 알고리즘은 그림 6처럼 되는데 그림5의  등식을 보면 이해가 갈 것이다. 

그림6

이것을 사용하여 위의 다항식 계산에 적용한다면 그림7와 같은 계산과정을 거치게 된다.

 

그림7

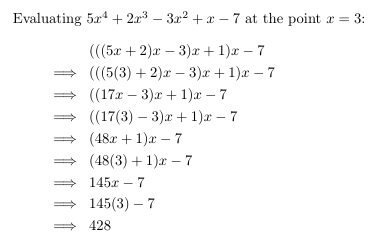
호너의 법칙을 이용하여 구현한 코드는 다음과 같다.

 
public class Polynomial {
 
 
    /**
     * @param  coefficients 는 다항식 각 차수의 계수이다.
     * @param x
     * */
    public static void computePolynomial(double[] coefficients, double x) {
 
        int totalAdditions = 0;
        int totalMultiplications = 0;
 
        int n = coefficients.length - 1;
        double result = coefficients[n];
 
        for (int i = n-1; i >= 0; i--) {
            result = (result * x) + coefficients[i];
            totalAdditions += 1;
            totalMultiplications += 1;
        }
 
        System.out.println(String.format("result=%.2f, " +
                "total addition = %d, " +
                "total multiplication = %d", result, totalAdditions, totalMultiplications));
    }
 
 
    public static void main(String[] args) {
        // Polynomial: 5x^4 + 2x^3 - 3x^2 + x - 7
        double[] examplePoly = new double[]{ -7, 1, -3, 2, 5 };
        Polynomial.computePolynomial(examplePoly, 3);
    }
 
}
 

 

그림8

 

참고로 호너의 법칙은 문자열 매칭 알고리즘인 라빈 카프 문자열 매칭 알고리즘(Rabin-Karp String Matching Algorithm) 에서 해싱값을 구할때 사용되기도 한다. 

레퍼런스

• wikipedia - Horner`s method
• Horner`s Rule for Polynomial Computation
• GeeksforGeeks - 호너의 법칙